 login/create account
login/create account
Makowsky, Janos A.
Blatter-Specker Theorem for ternary relations ★★
Author(s): Makowsky
Let 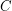 be a class of finite relational structures. We denote by
be a class of finite relational structures. We denote by 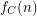 the number of structures in
the number of structures in 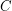 over the labeled set
over the labeled set 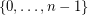 . For any class
. For any class 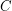 definable in monadic second-order logic with unary and binary relation symbols, Specker and Blatter showed that, for every
definable in monadic second-order logic with unary and binary relation symbols, Specker and Blatter showed that, for every 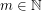 , the function
, the function 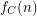 is ultimately periodic modulo
is ultimately periodic modulo  .
.
Question Does the Blatter-Specker Theorem hold for ternary relations.
Keywords: Blatter-Specker Theorem; FMT00-Luminy

 Drupal
Drupal CSI of Charles University
CSI of Charles University