Home » Subject » Logic » Finite Model Theory
Importance: Medium ✭✭
Author(s): Makowsky, Janos A.
Subject: Logic
» Finite Model Theory
Keywords: Blatter-Specker Theorem
FMT00-Luminy
Recomm. for undergrads: no
Posted by: dberwanger
on: May 18th, 2012

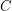Let $ C $ be a class of finite relational structures. We denote by 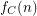$ f_C(n) $ the number of structures in 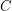$ C $ over the labeled set 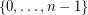$ \{0, \dots, n-1 \} $. For any class 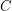$ C $ definable in monadic second-order logic with unary and binary relation symbols, Specker and Blatter showed that, for every 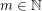$ m \in \mathbb{N} $, the function 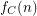$ f_C(n) $ is ultimately periodic modulo $ m $.

Question   Does the Blatter-Specker Theorem hold for ternary relations.

Our exposition follows closely [BS84].

Counting labeled structures modulo $ m $

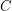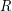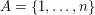
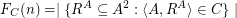
Let $ C $ be a class of finite structures for one binary relation symbol $ R $. We define for $ A = \{ 1, \ldots, n \} $ $$ F_C(n) = \mid \{ R^A \subseteq A^2 : \langle A, R^A \rangle \in C \} \mid $$

Examples:

    \item If 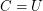$ C=U $ consists of all 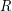$ R $-structures, 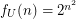$ f_U(n)= 2^{n^2} $. \item If 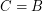$ C=B $ consists of bijections, 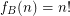$ f_B(n)= n! $ \item If 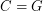$ C= G $ is the class of all (undirected, simple) graphs, 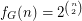$ f_G(n)= 2^{\binom{n}{2}} $. \item If 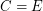$ C=E $ is the class of all equivalence relations, then 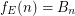$ f_E(n)= B_n $, the {\em Bell Numbers}. \item If 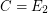$ C=E_2 $ is the class of all equivalence relations with two classes only, of the same size, 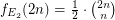$ f_{E_2}(2n)= \frac{1}{2} \cdot {\binom{2n}{n}} $. Clearly, 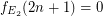$ f_{E_2}(2n+1)= 0 $. \item If 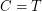$ C=T $ is the class of all trees, 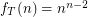$ f_T(n)= n^{n-2} $, {\em Caley}.

We observe the following:

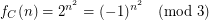
$$f_C(n)= 2^{n^2} = (-1)^{n^2} \pmod{3}$$

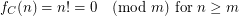
$$f_C(n)= n! = 0 \pmod{m} \mbox{ for } n \geq m$$

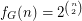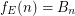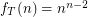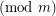And for each $ m $ the functions, $ f_G(n)= 2^{\binom{n}{2}} $, $ f_E(n)= B_n $, $ f_T(n)= n^{n-2} $ are ultimately periodic $ \pmod{m} $.

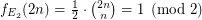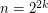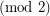However, $ f_{E_2}(2n)= \frac{1}{2} \cdot {\binom{2n}{n}} = 1 \pmod{2} $ iff $ n = 2^{2k} $, hence is not periodic $ \pmod{2} $.

Monadic second-order logic definable classes

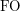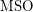The first four examples (all relations, all bijections, all graphs, all equivalence relations) are definable in First Order Logic $ \text{FO} $. The trees are definable in Monadic Second Order Logic $ \text{MSO} $..

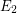$ E_2 $ is definable in Second Order Logic 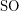$ \text{SO} $, but it is not 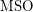$ \text{MSO} $-definable. If we expand 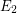$ E_2 $ to have the bijection between the classes we get structures with two binary relations. The class is now 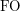$ \text{FO} $-definable. Let us denote the corresponding counting function 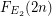$ F_{E_2}(2n) $. We have 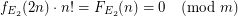$$ f_{E_2}(2n) \cdot n! = F_{E_2}(n) = 0 \pmod{m} $$ for $ n $ large enough.

Periodicity and linear recurrence relations

The periodicity of 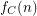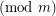$ f_C(n) $ $ \pmod{m} $ is usually established by exhibiting a linear recurrence relation:

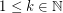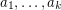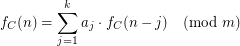
There exists $ 1 \leq k \in \mathbb{N} $ and integers $ a_1, \ldots, a_k $ such that for all $ n $ $$ f_C(n) = \sum_{j=1}^{k} a_j \cdot f_C(n-j) \pmod{m} $$

Examples.

    \item In the case of 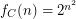$ f_C(n) = 2^{n^2} $ we have 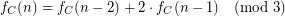$$ f_C(n) = f_C(n-2) + 2 \cdot f_C(n-1) \pmod{3} $$ \item In the case of 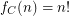$ f_C(n) = n! $ we have for all 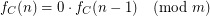$ m $ $$ f_C(n) = 0 \cdot f_C(n-1) \pmod{m} $$ In this case we say that 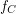$ f_C $ trivializes.

The Blatter-Specker Theorem

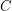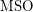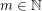
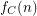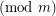Theorem  (BS84)   Let $ \tau $ be a binary vocabulary, i.e. all relation symbols are at most binary. If $ C $ is a class of finite $ \tau $-structures which is $ \text{MSO} $-definable, then for all $ m \in \mathbb{N} $ $ f_C(n) $ is ultimately periodic $ \pmod{m} $.

Moreover, there exists 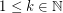$ 1 \leq k \in \mathbb{N} $ and integers 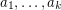$ a_1, \ldots, a_k $ such that for all 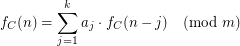$ n $ $$ f_C(n) = \sum_{j=1}^{k} a_j \cdot f_C(n-j) \pmod{m} $$ i.e we have a linear recurrence relation.

In [F03] Fischer showed that the Specker-Blatter Theorem does not hold for quaternary relations.

The case of ternary relations remains open.

See also [FM06] for further developments on the topic.

Bibliography

[BS84]* C. Blatter and E. Specker, Recurrence relations for the number of labeled structures on a finite set, Logic and Machines: Decision Problems and Complexity, E. Börger, G. Hasenjaeger and D. Rödding, eds, LNCS 171 (1984) pp. 43-61.

[F03] E. Fischer, The Specker-Blatter theorem does not hold for quaternary relations, Journal of Combinatorial Theory Series A 103(2003), 121-136.

[FM06] E. Fischer and J. A. Makowsky, The Specker-Blatter Theorem revisited: Generating functions for definable classes of stuctures. In Computing and Combinatorics (COCOON 2003) Proc., LNCS vol. 2697 (2003), 90-101.

[S88] E. Specker, Application of Logic and Combinatorics to Enumeration Problems, Trends in Theoretical Computer Science, E. Börger ed., Computer Science Press, 1988, pp. 141-169. Reprinted in: Ernst Specker, Selecta, Birkhäuser 1990, pp. 324-350.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options