 login/create account
login/create account
nowhere-zero flows
Circular flow numbers of $r$-graphs ★★
Author(s): Steffen
A nowhere-zero  -flow
-flow 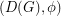 on
on  is an orientation
is an orientation 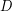 of
of  together with a function
together with a function 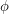 from the edge set of
from the edge set of  into the real numbers such that
into the real numbers such that 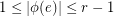 , for all
, for all 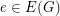 , and
, and 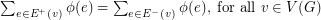 .
.
A 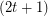 -regular graph
-regular graph  is a
is a 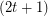 -graph if
-graph if 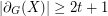 for every
for every 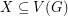 with
with 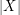 odd.
odd.
Conjecture Let 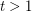 be an integer. If
be an integer. If  is a
is a 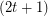 -graph, then
-graph, then 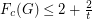 .
.
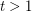 be an integer. If
be an integer. If  is a
is a 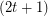 -graph, then
-graph, then 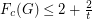 .
. Keywords: flow conjectures; nowhere-zero flows

 Drupal
Drupal CSI of Charles University
CSI of Charles University