 login/create account
login/create account
A nowhere-zero  -flow
-flow 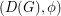 on
on  is an orientation
is an orientation  of
of  together with a function
together with a function 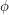 from the edge set of
from the edge set of  into the real numbers such that
into the real numbers such that 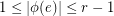 , for all
, for all 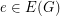 , and
, and 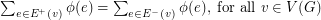 .
.
A 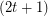 -regular graph
-regular graph  is a
is a 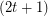 -graph if
-graph if 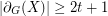 for every
for every 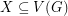 with
with 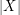 odd.
odd.
Conjecture Let 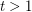 be an integer. If
be an integer. If  is a
is a 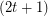 -graph, then
-graph, then 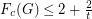 .
.
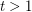 be an integer. If
be an integer. If  is a
is a 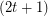 -graph, then
-graph, then 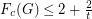 .
.
Since every 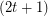 -regular class 1 graph is a
-regular class 1 graph is a 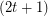 -graph, the truth of this conjecture would imply the truth of the conjecture on the circular flow number of regular class 1 graphs. If it is true for even
-graph, the truth of this conjecture would imply the truth of the conjecture on the circular flow number of regular class 1 graphs. If it is true for even 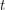 , say
, say 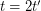 , then Jaeger's modular orientation conjecture is true for
, then Jaeger's modular orientation conjecture is true for 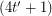 -regular graphs and hence, by a result of Jaeger, it would imply the truth of Tutte's 5-flow conjecture. For
-regular graphs and hence, by a result of Jaeger, it would imply the truth of Tutte's 5-flow conjecture. For 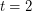 it is Tutte's 3-flow conjecture.
it is Tutte's 3-flow conjecture.
Bibliography
*[ES_2015]E. Steffen, Edge-colorings and circular flow numbers on regular graphs, J. Graph Theory 79, 1–7, 2015
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University