 login/create account
login/create account
total order
Chain-meet-closed sets ★★
Author(s): Porton
Let  is a complete lattice. I will call a filter base a nonempty subset
is a complete lattice. I will call a filter base a nonempty subset  of
of  such that
such that 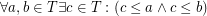 .
.
Definition A subset  of a complete lattice
of a complete lattice  is chain-meet-closed iff for every non-empty chain
is chain-meet-closed iff for every non-empty chain 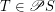 we have
we have 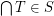 .
.
 of a complete lattice
of a complete lattice  is chain-meet-closed iff for every non-empty chain
is chain-meet-closed iff for every non-empty chain 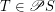 we have
we have 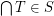 .
. Conjecture A subset  of a complete lattice
of a complete lattice  is chain-meet-closed iff for every filter base
is chain-meet-closed iff for every filter base 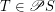 we have
we have 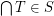 .
.
 of a complete lattice
of a complete lattice  is chain-meet-closed iff for every filter base
is chain-meet-closed iff for every filter base 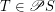 we have
we have 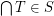 .
. Keywords: chain; complete lattice; filter bases; filters; linear order; total order

 Drupal
Drupal CSI of Charles University
CSI of Charles University