 login/create account
login/create account
Grotzsch proved that every triangle free (and loopless) planar graph is 3-colorable. By flow/coloring duality, this is equivalent to the statement that every 4-edge-connected planar graph has a nowhere-zero 3-flow. The 3-flow conjecture asserts that this is still true without the assumption of planarity.
Jaeger proved that 4-edge-connected graphs have nowhere-zero 4-flows, but very little is known about nowhere-zero 3-flows. In particular, the following weak version of the 3-flow conjecture is still wide open.
 so that every
so that every  -edge-connected graph has a nowhere-zero 3-flow.
-edge-connected graph has a nowhere-zero 3-flow. Lai and Zhang [LZ] have proved that if  has
has  vertices and edge-connectivity at least
vertices and edge-connectivity at least 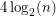 then
then  has a nowhere-zero 3-flow. A similar result (edge connectivity at least
has a nowhere-zero 3-flow. A similar result (edge connectivity at least 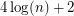 ) also follows from a theorem of Alon, Linial, and Meshulam [ALM] on additive bases of vector spaces.
) also follows from a theorem of Alon, Linial, and Meshulam [ALM] on additive bases of vector spaces.
Bibliography
[ALM] N. Alon, N. Linial, and R. Meshulam Additive Bases of Vector Spaces over Prime Fields J. Combinatorial Theory Ser. A 57 (1991), 203-210.
[J] F. Jaeger, Flows and Generalized Coloring Theorems in Graphs, J. Combinatorial Theory Ser. B 26 (1979) 205-216.
[LZ] H.J. Lai and C.Q. Zhang, Nowhere-Zero 3-Flows of Highly Connected Graphs, Discrete Math 110 (1992) 179-183.
[T54] W.T. Tutte, A Contribution on the Theory of Chromatic Polynomial, Canad. J. Math. 6 (1954) 80-91.
[T66] W.T. Tutte, On the Algebraic Theory of Graph Colorings, J. Combinatorial Theory 1 (1966) 15-50.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University