Open Problem Garden

The Four Color Theorem is equivalent to the statement that every cubic planar graph with no bridge is 3-edge-colorable. This is precisely equivalent to Grunbaum's conjecture restricted to the plane. Thus, Grunbaum's conjecture, if true, would imply the Four Color Theorem. Indeed, this conjecture suggests a deep generalization of the 4-color theorem.

Definition: A cubic graph is a snark if is internally 4-edge-connected and is not 3-edge-colorable.

Grunbaum's conjecture states that no snark is the dual of a simple loopless triangulation of an orientable surface. In this light, the conjecture looks to be almost obviously false. To find a counterexample, it suffices to embed a snark in an orientable surface so that the dual has no loops or parallel edges. Of course, the difficulty is in satisfying this last constraint. All known embeddings of snarks in orientable surfaces give rise to either loops or parallel edges in the dual. It is striking to compare this conjecture with the Orientable cycle double cover conjecture. Both conjectures may be stated in terms of embedding snarks in orientable surfaces as follows:

In this light it may look unlikely that both Grunbaum's conjecture and the orientable cycle double cover conjecture are true. I (M. DeVos) don't have a strong sense for or against either of these conjectures, and I don't believe there is a strong consensus among experts.

Mohar and Robertson have suggested the following weak version of Grunbaum's conjecture: There exists a fixed constant so that the dual of every loopless triangulation of an orientable surface of face-width 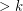is 3-edge-colorable. Robertson has suggested that this may still hold true even for nonorientable surfaces. The following conjecture is a further weakening of Grunbaum's conjecture which would allow the parameter to depend on the surface. This is probably the weakest open problem in this vein.

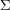Conjecture  (Weak Grunbaum conjecture)   For every orientable surface , there is a fixed constant so that the dual of every loopless triangulation of 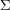with face-width 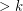is 3-edge-colorable.