Home » Subject » Unsorted
Importance: Medium ✭✭
Author(s): Porton, Victor
Subject: Unsorted
Keywords: complete lattice
filter
Recomm. for undergrads: no
Posted by: porton
on: July 31st, 2009
Solved by: Blass, Andreas

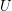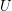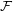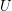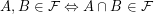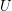Let $ U $ is a set. A filter (on $ U $) $ \mathcal{F} $ is by definition a non-empty set of subsets of $ U $ such that $ A,B\in\mathcal{F} \Leftrightarrow A\cap B\in\mathcal{F} $. Note that unlike some other authors I do not require $ \varnothing\notin\mathcal{F} $. I will denote $ \mathscr{F} $ the lattice of all filters (on $ U $) ordered by set inclusion.

Let 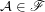$ \mathcal{A}\in\mathscr{F} $ is some (fixed) filter. Let 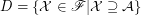$ D=\{\mathcal{X}\in\mathscr{F} | \mathcal{X}\supseteq \mathcal{A}\} $. Obviously $ D $ is a bounded lattice.

I will call complementive such filters 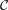$ \mathcal{C} $ that:

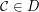  1. $ \mathcal{C}\in D $;
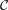  2. $ \mathcal{C} $ is a complemented element of the lattice $ D $.
Conjecture   The set of complementive filters ordered by inclusion is a complete lattice.

To this problem was found a counterexample in a MathOverflow question answer.

The counter example with a rewritten proof is also available in Filters on Posets and Generalizations online article.

Bibliography

*Victor Porton. Do filters complementive to a given filter form a complete lattice?


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options