 login/create account
login/create account
filter
Join of oblique products ★★
Author(s): Porton
Conjecture 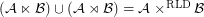 for every filter objects
for every filter objects 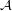 ,
, 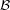 .
.
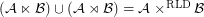 for every filter objects
for every filter objects 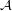 ,
, 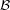 .
. Keywords: filter; oblique product; reloidal product
Do filters complementive to a given filter form a complete lattice? ★★
Author(s): Porton
Let 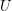 is a set. A filter (on
is a set. A filter (on 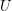 )
) 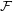 is by definition a non-empty set of subsets of
is by definition a non-empty set of subsets of 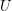 such that
such that 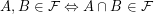 . Note that unlike some other authors I do not require
. Note that unlike some other authors I do not require 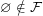 . I will denote
. I will denote 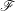 the lattice of all filters (on
the lattice of all filters (on 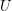 ) ordered by set inclusion.
) ordered by set inclusion.
Let 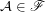 is some (fixed) filter. Let
is some (fixed) filter. Let 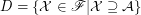 . Obviously
. Obviously 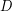 is a bounded lattice.
is a bounded lattice.
I will call complementive such filters 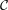 that:
that:
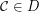 ;
;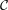 is a complemented element of the lattice
is a complemented element of the lattice 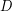 .
.
Conjecture The set of complementive filters ordered by inclusion is a complete lattice.
Keywords: complete lattice; filter

 Drupal
Drupal CSI of Charles University
CSI of Charles University