 login/create account
login/create account
Conjecture 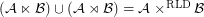 for every filter objects
for every filter objects 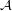 ,
, 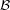 .
.
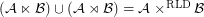 for every filter objects
for every filter objects 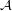 ,
, 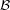 .
. See Algebraic General Topology for definitions of used concepts.
I proved it false based on a solution of an equivalent elementary problem by Andreas Blass.
Bibliography
*Victor Porton. Algebraic General Topology
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University