 login/create account
login/create account
Let  be a non-empty finite set. Given a partition
be a non-empty finite set. Given a partition 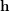 of
of  , the stabilizer of
, the stabilizer of 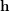 , denoted
, denoted 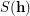 , is the group formed by all permutations of
, is the group formed by all permutations of  preserving each block of
preserving each block of 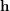 .
.
 ) Find a sufficient condition for a sequence of partitions
) Find a sufficient condition for a sequence of partitions 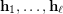 of
of  to be complete, i.e. such that the product of their stabilizers
to be complete, i.e. such that the product of their stabilizers 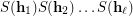 is equal to the whole symmetric group
is equal to the whole symmetric group  on
on  . In particular, what about completeness of the sequence
. In particular, what about completeness of the sequence 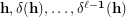 , given a partition
, given a partition 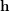 of
of  and a permutation
and a permutation  of
of  ?
? 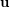 be a uniform partition of
be a uniform partition of  and
and 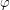 be a permutation of
be a permutation of  such that
such that 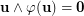 . Suppose that the set
. Suppose that the set 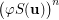 is transitive, for some integer
is transitive, for some integer 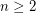 . Then
. Then 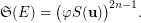
This conjecture was essentially proposed by Václav E. Beneš in 1975 [B75] and bears his name. It remains open for all 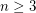 .
.
A partition of a set is uniform if all its blocks have the same size. Given a subset 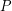 of a multiplicative group and a positive integer
of a multiplicative group and a positive integer  , by
, by 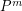 we mean the product
we mean the product 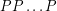 (
( times). A set
times). A set  is transitive if for every
is transitive if for every 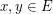 there exists a permutation
there exists a permutation  such that
such that 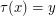 . The infinum of two partitions
. The infinum of two partitions  and
and  of
of  is the partition of
is the partition of  defined by
defined by
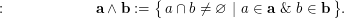
The partition 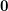 of
of  is defined by
is defined by 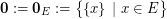 . So the condition
. So the condition 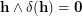 is equivalent to saying that for every pair of blocks
is equivalent to saying that for every pair of blocks 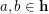 , the intersection
, the intersection 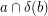 consists of at most one element.
consists of at most one element.
Observe that the decomposition 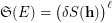 is equivalent to completeness of the sequence
is equivalent to completeness of the sequence 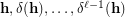 due to the obvious identity
due to the obvious identity 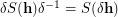 . Thus Problem (
. Thus Problem ( ) is indeed underlying for Beneš conjecture.
) is indeed underlying for Beneš conjecture.
Problem ( ) is a special case of a broader fundamental problem of description of product of stabilizers on a finite set. The latter problem, which I believe is combinatorial by nature, is of great interest in switching network study. However, despite many years of extensive research on its various cases in the context of switching networks, this fascinating problem remains unsolved in all but a very few interesting instances. Very little is understood about such products beyond what is obvious. In particular, it is unclear how to efficiently compute their cardinalities. Even for some rather simple sequences of partitions, the product of their stabilizers is surprisingly difficult to describe. Beneš conjecture, if proven (even under some additional assumptions on
) is a special case of a broader fundamental problem of description of product of stabilizers on a finite set. The latter problem, which I believe is combinatorial by nature, is of great interest in switching network study. However, despite many years of extensive research on its various cases in the context of switching networks, this fascinating problem remains unsolved in all but a very few interesting instances. Very little is understood about such products beyond what is obvious. In particular, it is unclear how to efficiently compute their cardinalities. Even for some rather simple sequences of partitions, the product of their stabilizers is surprisingly difficult to describe. Beneš conjecture, if proven (even under some additional assumptions on  ), would provide a very useful and easy-to-check sufficient condition for completeness of the sequences
), would provide a very useful and easy-to-check sufficient condition for completeness of the sequences 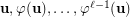 that are of particular interest.
that are of particular interest.
Another important and interesting problem related to ( ) is to find an efficient polynomial-time (in
) is to find an efficient polynomial-time (in 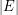 ) factorization algorithm for the identity
) factorization algorithm for the identity 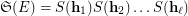 . Given an identity
. Given an identity 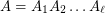 , where all
, where all 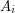 are subsets of a multiplicative group, a factorization algorithm finds for every
are subsets of a multiplicative group, a factorization algorithm finds for every 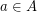 an
an 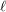 -tuple
-tuple 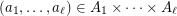 such that
such that 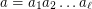 .
.
Beneš conjecture is mainly famous for its central case, Shuffle-Exchange (SE) conjecture, stating essentially that 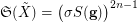 , where
, where 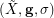 is an instance of
is an instance of 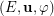 defined, given arbitrary integer parameters
defined, given arbitrary integer parameters 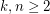 , as follows:
, as follows:

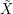 is the set of all words of length
is the set of all words of length  over a
over a  -letter alphabet
-letter alphabet 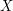 .
.

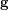 is the
is the 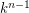 -partition of
-partition of 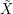 formed by the equivalence relation
formed by the equivalence relation 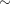 on
on 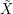 defined by
defined by
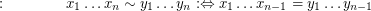 .
.

 is the shuffle permutation of
is the shuffle permutation of  defined by
defined by 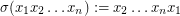 .
.
Whereas SE conjecture, especially its case 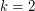 , has received enormous attention in the study of switching networks with relatively little progress, the general case of Beneš conjecture, despite importance of Problem (
, has received enormous attention in the study of switching networks with relatively little progress, the general case of Beneš conjecture, despite importance of Problem ( ) in that area, has virtually generated no literature and had no progress. While I strongly believe in the validity of SE conjecture, I am not so sure about the general case of Beneš conjecture and even do not rule out that it could be disproved by a low-scale counterexample. On the other hand, I cannot rule out that Beneš conjecture (possibly under some mild additional assumptions on
) in that area, has virtually generated no literature and had no progress. While I strongly believe in the validity of SE conjecture, I am not so sure about the general case of Beneš conjecture and even do not rule out that it could be disproved by a low-scale counterexample. On the other hand, I cannot rule out that Beneš conjecture (possibly under some mild additional assumptions on 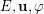 ) may be reduced to SE conjecture.
) may be reduced to SE conjecture.
It is easy to see that the case  of Beneš conjecture coincides with that of SE conjecture. The latter case is well known to be valid (discussed here).
of Beneš conjecture coincides with that of SE conjecture. The latter case is well known to be valid (discussed here).
Unlike completeness of a sequence of partitions of  , the condition of transitivity of the product of their stabilizers is very easy to check. In particular, transitivity of the set
, the condition of transitivity of the product of their stabilizers is very easy to check. In particular, transitivity of the set 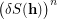 with
with 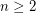 is equivalent to the following assertion:
is equivalent to the following assertion:
![$$ :\qquad\qquad \forall\,h_1,h_n\in{\bf h} \ \exists\,h_2,\dots,h_{n-1}\in{\bf h} \ \forall\, i\in[n-1]: h_i\cap \delta(h_{i+1}) \ne \varnothing. $$](/files/tex/0eaf6ecf837891cbbc1875fb6f3844909fce56f1.png)
Beneš conjecture (as well as its underlying Problem ( ) and a broader problem of description of product of stabilizers on a finite set) admits a nice equivalent graph-theoretic form.
) and a broader problem of description of product of stabilizers on a finite set) admits a nice equivalent graph-theoretic form.
Counterexamples
In what follows we present 3 counterexamples showing that certain stronger versions of Beneš conjecture are false.
Counterexample 1. The condition 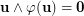 is necessary for Beneš conjecture. This can be shown by the following simple counterexample:
is necessary for Beneš conjecture. This can be shown by the following simple counterexample:
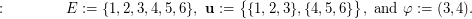
Indeed, 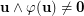 as
as 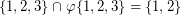 . Also, the set
. Also, the set 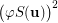 is obviously transitive. However, it can be easily seen that any permutation
is obviously transitive. However, it can be easily seen that any permutation  of
of  satisfying
satisfying 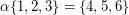 does not belong to
does not belong to 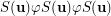 . Thus,
. Thus, 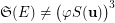 . In fact, the condition
. In fact, the condition 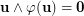 is missing in the original statement [B75] of Beneš conjecture (however, such condition is commonly (but not always) assumed in the context of switching networks).
is missing in the original statement [B75] of Beneš conjecture (however, such condition is commonly (but not always) assumed in the context of switching networks).
Counterexample 2. Beneš conjecture is not directly generalizable to the products of stibilizers of the form 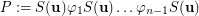 . More precisely, transitivity of
. More precisely, transitivity of 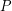 does not always imply
does not always imply 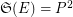 , where
, where 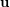 is a uniform partition of
is a uniform partition of  and all
and all 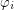 are permutations of
are permutations of  such that
such that 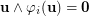 (while Beneš conjecture states that this implication is always true as long as
(while Beneš conjecture states that this implication is always true as long as 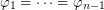 ). For that I constructed the following counterexample:
). For that I constructed the following counterexample:
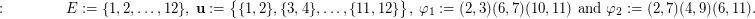
Indeed, it is obvious that both permutations 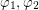 are satisfying
are satisfying 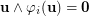 and the set
and the set 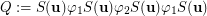 is transitive. However,
is transitive. However, 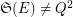 as, in particular, it can be easily seen that any permutation
as, in particular, it can be easily seen that any permutation  of
of  satisfying
satisfying 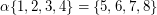 does not belong to
does not belong to 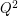 .
.
Counterexample 3. In the same paper [B75], Beneš also proposed the following
 ) Let
) Let 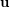 be a uniform partition of
be a uniform partition of  and
and 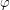 be a permutation of
be a permutation of  such that
such that 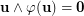 . Suppose that
. Suppose that 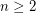 is the smallest integer such that the set
is the smallest integer such that the set 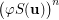 is transitive. Then
is transitive. Then 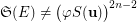 .
. In other words, this conjecture together with Beneš one, asserts that if 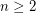 is the smallest integer such that
is the smallest integer such that 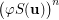 is transitive, then
is transitive, then 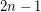 is the the smallest integer
is the the smallest integer 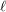 such that
such that 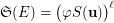 . However, Conjecture (
. However, Conjecture ( ) turned out to be generally false as I found the following counterexample for it:
) turned out to be generally false as I found the following counterexample for it:
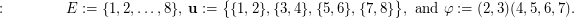
Indeed, it is easy to verify that 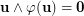 and the set
and the set 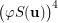 is transitive while
is transitive while 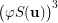 is not as, in particular,
is not as, in particular, 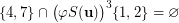 . However, a brute force verification confirmed that
. However, a brute force verification confirmed that 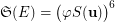 .
.
Bibliography
*[B75] V.E. Beneš, Proving the rearrangeability of connecting networks by group calculation, Bell Syst. Tech. J. 54 (1975), 421-434.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University