(Using instead of ) In [S], Soifer derives . As he mentioned, one can improve the covering construction. Holding the square of side length in the lower left corner, putting a square of side length in the upper right corner, covering the remaining uncovered area by 2 polyomino-coverings of rectangles of sides by , removing useless unit squares in polyominos, we get a lower bound for the rhs of that inequality: Denote by the minimal value of this expression when varying from 2 to . Results of computer calculations: iff or . For growing (checked up to ), for the lowest optimal , seems to converge to 1, and seems to converge to 3/4.
A lower bound of the upper bound from polyomino-covering in [S]
(Using instead of
instead of  )
)
In [S], Soifer derives ![$ \Pi(n) < (n-k)^2+2(k+1)[[\frac{k^2-1}{k^2+k-\sqrt{2k+2}} n]] $](/files/tex/97f11f1771afcd45f92827714150f8faa670556b.png) .
.
As he mentioned, one can improve the covering construction. Holding the square of side length 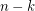 in the lower left corner, putting a square of side length
in the lower left corner, putting a square of side length  in the upper right corner, covering the remaining uncovered area by 2 polyomino-coverings of rectangles of sides
in the upper right corner, covering the remaining uncovered area by 2 polyomino-coverings of rectangles of sides 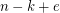 by
by 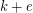 , removing useless unit squares in polyominos, we get a lower bound for the rhs of that inequality:
, removing useless unit squares in polyominos, we get a lower bound for the rhs of that inequality:
![$ (n-k)^2+k^2+2[[(k+1)(n-k)\frac{k^2-1}{k^2+k-\sqrt{2k+2}} ]] $](/files/tex/53e7346a9ad68ddeeebc33a5a499c0cd30365936.png)
Denote by 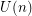 the minimal value of this expression when varying
the minimal value of this expression when varying  from 2 to
from 2 to 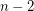 .
.
Results of computer calculations:
 iff
iff 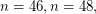 or
or  .
.
For growing  (checked up to
(checked up to 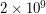 ), for the lowest optimal
), for the lowest optimal  ,
, 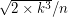 seems to converge to 1, and
seems to converge to 1, and 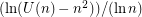 seems to converge to 3/4.
seems to converge to 3/4.