 login/create account
login/create account
Does there exist a planar graph with obstacle number greater than 1? Is there some  such that every planar graph has obstacle number at most
such that every planar graph has obstacle number at most  ?
?
A  -obstacle drawing of a graph
-obstacle drawing of a graph  is a mapping of the vertices of
is a mapping of the vertices of  to points in the plane, along with a set of polygonal obstacles
to points in the plane, along with a set of polygonal obstacles  , such that two vertices are adjacent precisely if the line segment connecting their corresponding points in
, such that two vertices are adjacent precisely if the line segment connecting their corresponding points in 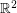 does not intersect any obstacle. The {\em obstacle number} of a graph
does not intersect any obstacle. The {\em obstacle number} of a graph  is the minimum
is the minimum  such that
such that  has a
has a  -obstacle drawing.
-obstacle drawing.
This invariant was recently introduced by Alpert, Koch, and Laison [AKL], who proved that every outerplanar graph has obstacle number 1. The next question, then, follows naturally: what is the obstacle number of a planar graph? So far no planar graph has been proved to have obstacle number greater than 1. Alpert, Koch, and Laison specifically ask what the obstacle numbers of the icosahedron and dodecahedron are [AKL].
Bibliography
[AKL] Hannah Alpert, Christina Koch, and Joshua D. Laison: Obstacle numbers of graphs. Discrete Comput. Geom. (2010) 44:223-244.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University