 login/create account
login/create account
 such that every
such that every  -arc-strong digraph
-arc-strong digraph 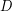 with specified vertices
with specified vertices  and
and  contains an out-branching rooted at
contains an out-branching rooted at  and an in-branching rooted at
and an in-branching rooted at  which are arc-disjoint.
which are arc-disjoint.
Thomassen [T] showed that, given a digraph 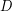 and two vertices
and two vertices  and
and  , deciding whether there are an out-branching rooted at
, deciding whether there are an out-branching rooted at  and an in-branching rooted at
and an in-branching rooted at  which are arc-disjoint is NP-complete.
which are arc-disjoint is NP-complete.
In contrast, one can decide in polynomial time whether there are  arc-disjoint out-branchings with specified roots
arc-disjoint out-branchings with specified roots 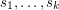 (some of which may be identical). This is a consequence of Edmonds’ well known branching theorem [E] states that a digraph
(some of which may be identical). This is a consequence of Edmonds’ well known branching theorem [E] states that a digraph  has
has  arc-disjoint out-branchings rooted at some fixed vertex
arc-disjoint out-branchings rooted at some fixed vertex  if and only if there are
if and only if there are  arc-disjoint paths from
arc-disjoint paths from  to every other vertex of
to every other vertex of 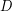 .
.
Bang-Jensen [B] proved this conjecture for tournaments.
A similar question can be asked about arc-disjoint strongly connected spanning subdigraphs. Several related problems are mentioned in the survey of Bang-Jensen and Kriesell [BK].
Bibliography
[B] J. Bang-Jensen, Edge-disjoint in- and out-branching in tournaments and related path problems. J. Combin. Theory Ser. B 51 (1991), 1-23.
[BK] J. Bang-Jensen, M. Kriesell, Disjoint sub(di)graphs in digraphs, Electronic Notes in Discrete Mathematics 34 (2009), 179-183.
[E] J. Edmonds, Edge-disjoint branchings. In Combinatorial Algorithms, B. Rustin, ed., Acad. Press, New York (1973), 91-96.
*[T] C. Thomassen, Configurations in Graphs, Annals of The New York Acad. Sci. 555 (1989), 402-412.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University