login/create account
Conjecture Every planar graph without 4-cycles and 5-cycles is 3-colourable.
Borodin et al. [BGRS] who proved that every planar graph without cycles of length in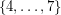 
is 3-colourable.
Borodin and Raspaud [BR] proposed the following conjecture which implies Steinberg's Conjecture.
Conjecture (Strong Bordeaux Conjecture) Every planar graph without 5-cycles and without adjacent triangles is 3-colourable.
This conjecture is in turn implied by the following stronger one due to Borodin et al. [BGJR]
Conjecture Every planar graph without 3-cycles adjacent to cycles of length 3 or 5 is 3-colourable.
Borodin et al. [BGJR06] proved that every planar graph without triangles adjacent to cycles of length from 3 to 9 is 3-colourable.
Steinberg's Conjecture cannot been generalized to list colouring: Voigt [V] constructed a planar graph without 4-cycles and 5-cycles which is not 3-choosable.
Bibliography
[BGJR] O.V. Borodin, A.N. Glebov, T.R. Jensen, and A.Raspaud. Planar graphs without triangles adjacent to cycles of length from 3 to 9 are 3-colorable. Sib. Elektron. Mat. Izv., 3:428--440, 2006.
[BGRS] O. V. Borodin, A. N. Glebov, A. Raspaud, and M. R. Salavatipour. Planar graphs without cycles of length from 4 to 7 are 3-colorable. J. Combin. Theory Ser. B, 93(2):303--311, 2005.
[BR] O. V. Borodin and A. Raspaud. A sufficient condition for planar graphs to be 3-colorable. J. Combin. Theory Ser. B, 88(1):17--27, 2003.
[V] M. Voigt. A non-3-choosable planar graph without cycles of length 4 and 5. Discrete Math., 307(7-8):1013--1015, 2007.
* indicates original appearance(s) of problem.
Drupal
CSI of Charles University