 login/create account
login/create account
Let  denote the residue class
denote the residue class  . A covering system (defined by Paul Erdos in early 1930's) is a finite collection
. A covering system (defined by Paul Erdos in early 1930's) is a finite collection  of residue classes whose union covers all the integers. Such systems are easy to find if the moduli are allowed to repeat, or if we allow even numbers. The covering system is called incongruent if all the moduli are distinct.
of residue classes whose union covers all the integers. Such systems are easy to find if the moduli are allowed to repeat, or if we allow even numbers. The covering system is called incongruent if all the moduli are distinct.
Partial results are known. Berger, Felzenbaum and Fraenkel ([BFF1], [BFF2]) show (among else) that if covering system with odd distinct moduli (greater than 1) exists, 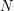 is the least common multiple of
is the least common multiple of  , \dots,
, \dots, 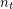 , and
, and 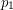 , \dots,
, \dots, 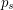 are all distinct prime divisors of~
are all distinct prime divisors of~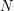 , then
, then 
Simpson and Zeilberger [SZ] proved that if in addition  , \dots ,
, \dots , 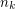 are square-free, then
are square-free, then 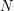 has at least 18 prime divisors.
has at least 18 prime divisors.
Guo and Sun [GS] recently improved this to show that if 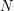 is square-free, then it has at least 22 prime divisors.
is square-free, then it has at least 22 prime divisors.
Bibliography
[BFF1] M. A. Berger, A. Felzenbaum and A. S. Fraenkel, Necessary condition for the existence of an incongruent covering system with odd moduli, Acta. Arith. 45 (1986), 375–379
[BFF2] M. A. Berger, A. Felzenbaum and A. S. Fraenkel, Necessary condition for the existence of an incongruent covering system with odd moduli. II, Acta Arith. 48 (1987), 73–79.
[GS] Song Guo and Zhi-Wei Sun: On odd covering systems with distinct moduli; Adv. Appl. Math. 35(2005), 182–187
[SZ] R. J. Simpson and D. Zeilberger, Necessary conditions for distinct covering systems with square-free moduli, Acta. Arith. 59 (1991), 59–70.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University