Open Problem Garden

Importance: Medium ✭✭

Author(s):	Havet, Frédéric
	Maia, Ana Karolinna

Subject:	Graph Theory
	» Directed Graphs

Keywords:

Recomm. for undergrads: no

Posted	by:	fhavet
	on:	June 25th, 2013

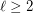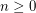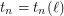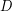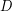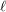Conjecture Let $\ell \geq 2$ be an integer. For every integer $n\geq 0$ , there exists an integer $t_n=t_n(\ell)$ such that for every digraph $D$ , either $D$ has a $n$ pairwise-disjoint directed cycles of length at least $\ell$ , or there exists a set $T$ of at most 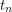$t_n$ vertices such that 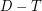$D-T$ has no directed cycles of length at least $\ell$ .

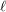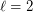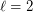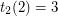The case $\ell=2$ has been proved by Reed et al. [RRST], hence solving a conjecture of Gallai [G] and Younger [Y]. The case $\ell=2$ and $n=2$ has previously been solved by McCuaig [M], who proved that $t_2(2)=3$ . Havet and Maia [HM] proved the case $\ell=3$ .

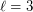The analogous statement for undirected graph has been proved by Birmelé, Bondy and Reed [BBR], hence generalizing Erdős-Posa [EP] result for 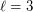$\ell =3$ .

Bibliography

[BBR] E. Birmelé, J.A. Bondy, and B.A. Reed. The Erdos-Posa property for long circuits, Combinatorica, 27(2), 135–145, 2007.

[EP] P. Erdős and L. Pósa. On the independent circuits contained in a graph. Canad. J. Math., 17, 347--352, 1965.

[G] T. Gallai. Problem 6, in Theory of Graphs, Proc. Colloq. Tihany 1966 (New York), Academic Press, p.362, 1968.

*[HM] F. Havet and A. K. Maia. On disjoint directed cycles with prescribed minimum lengths. INRIA Research Report, RR-8286, 2013.

[M] W. McCuaig, Intercyclic digraphs. Graph Structure Theory, (Neil Robertson and Paul Seymour, eds.), AMS Contemporary Math., 147:203--245, 1993.

[RRST] B. Reed, N. Robertson, P.D. Seymour, and R. Thomas. Packing directed circuits. Combinatorica, 16(4):535--554, 1996.

[Y] D. H. Younger. Graphs with interlinked directed circuits. Proceedings of the Midwest Symposium on Circuit Theory, 2:XVI 2.1 - XVI 2.7, 1973.

* indicates original appearance(s) of problem.

add new comment

Open Problem Garden

Bibliography

Reply

Navigate

Recent Activity