 login/create account
login/create account
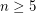 ,
, 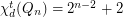 .
.
Here  denotes the
denotes the  -dimensional hypercube, i.e. the graph with vertex set
-dimensional hypercube, i.e. the graph with vertex set 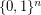 and two vertices adjacent if they differ in exactly one coordinate. A total dominator coloring of a graph
and two vertices adjacent if they differ in exactly one coordinate. A total dominator coloring of a graph  , briefly TDC, is a proper coloring of
, briefly TDC, is a proper coloring of  in which each vertex of the graph is adjacent to every vertex of some color class. The total dominator chromatic number
in which each vertex of the graph is adjacent to every vertex of some color class. The total dominator chromatic number 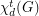 of
of  is the minimum number of color classes in a TDC in
is the minimum number of color classes in a TDC in  (see [Kaz1]). A total dominating set of a graph
(see [Kaz1]). A total dominating set of a graph  is a set
is a set  of vertices of
of vertices of  such that every vertex has at least one neighbor in
such that every vertex has at least one neighbor in  ". The total domination number
". The total domination number 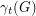 of
of  is the cardinality of a minimum total dominating set.
is the cardinality of a minimum total dominating set.
The following theorems are proved in [Kaz2].
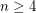 ,
, 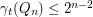 .
. 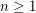 ,
, 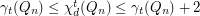 .
. 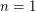 , then
, then 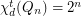 .
. 2. If
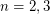 , then
, then  .
. 3. If
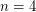 , then
, then 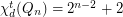 .
. Bibliography
[Kaz1] Adel P. Kazemi, Total dominator chromatic number of a graph, http://arxiv.org/abs/1307.7486.
[Kaz2] Adel P. Kazemi, Total Dominator Coloring in Product Graphs, Utilitas Mathematica (2013), Accepted.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University