 login/create account
login/create account
 , every digraph with minimum out-degree at least
, every digraph with minimum out-degree at least  contains
contains  disjoint cycles.
disjoint cycles.
This conjecture is a simple observation when  . It was proved by Thomassen~[Tho83] in 1983 when
. It was proved by Thomassen~[Tho83] in 1983 when 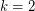 , and more recently the case
, and more recently the case 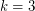 was settled~[LPS07].
was settled~[LPS07].
The bound offered would be optimal — just consider a symmetric complete graph on  vertices. In 1996, Alon~[Alo96] proved that the statement is true with
vertices. In 1996, Alon~[Alo96] proved that the statement is true with  replaced by
replaced by 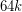 . The conjecture was also verified for tournaments of minimum in-degree at least
. The conjecture was also verified for tournaments of minimum in-degree at least  ~[BLS07].
~[BLS07].
Bang-Jensen et al. [BBT] made a stronger conjecture for digraph with sufficiently large girth.
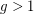 , every digraph
, every digraph  with girth at least
with girth at least  and with minimum out-degree at least
and with minimum out-degree at least  contains
contains  disjoint cycles.
disjoint cycles. The constant 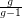 is best possible. Indeed, for every integers
is best possible. Indeed, for every integers 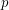 and
and  , consider the digraph
, consider the digraph 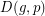 on
on 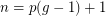 vertices with vertex set
vertices with vertex set 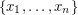 and arc set
and arc set  . It has girth
. It has girth  and out-degree
and out-degree 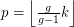 . Moreover, for
. Moreover, for  , the digraph
, the digraph 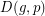 admits a partition into
admits a partition into  vertex disjoint 3-cycles and no more. For g = 3, the first case of this conjecture which differs from Bermond-Thomassen Conjecture and which is not already known corresponds to the following question:
vertex disjoint 3-cycles and no more. For g = 3, the first case of this conjecture which differs from Bermond-Thomassen Conjecture and which is not already known corresponds to the following question:
Bibliography
[Alo96] N. Alon: Disjoint directed cycles, J. Combin. Theory Ser. B, 68(2):167--178, 1996. PDF
[BBT] J. Bang-Jensen, S. Bessy and S. Thomassé, Disjoint 3-cycles in tournaments: a proof of the Bermond-Thomassen conjecture for tournaments, J. Graph Theory, to appear.
*[BeTh81] J.-C. Bermond and C.~Thomassen: Cycles in digraphs---a survey, J. Graph Theory, 5(1):1--43, 1981. MathSciNet
[BLS07] S.~Bessy, N.~Lichiardopol, and J.-S. Sereni: Two proofs of the {B}ermond-{T}homassen conjecture for tournaments with bounded minimum in-degree, Discrete Math., Special Issue dedicated to CS06, to appear.
[LPS07] N.~Lichiardopol, A.~ P\'or, and J.-S. Sereni: A step towards the Bermond-Thomassen conjecture about disjoint cycles in digraphs, Submitted, 2007.
[Tho83] C.~Thomassen, Disjoint cycles in digraphs, Combinatorica, 3(3-4):393--396, 1983. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University