Open Problem Garden

Importance: Medium ✭✭

Author(s):	Kloks, Ton
	Lee, Chuan-Min
	Liu, Jiping

Subject:	Graph Theory
	» Basic Graph Theory
	» » Cycles

Keywords:	cycle packing
	feedback vertex set
	planar graph

Recomm. for undergrads: no

Posted	by:	cmlee
	on:	October 9th, 2007

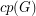For a graph $G$ , let $cp(G)$ denote the cardinality of a maximum cycle packing (collection of vertex disjoint cycles) and let 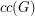$cc(G)$ denote the cardinality of a minimum feedback vertex set (set of vertices 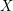$X$ so that 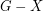$G-X$ is acyclic).

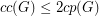Conjecture For every planar graph $G$ , $cc(G)\leq 2cp(G)$ .

In [KLL], the authors mention that there exists a family of nonplanar graphs for which 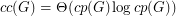$cc(G) = \Theta( cp(G) \log cp(G) )$ , so no such result could hold for general graphs. They also point out that the conjecture is tight for wheels, and they prove it for the special case of outerplanar graphs.

Bibliography

*[KLL] Ton Kloks, Chuan-Min Lee, and Jiping Liu, New Algorithms for $k$ -Face Cover, $k$ -Feedback Vertex Set, and $k$ -Disjoint Cycles on Plane and Planar Graphs, in Proceedings of the 28th International Workshop on Graph-Theoretic Concepts in Computer Science (WG2002), LNCS 2573, pp. 282--295, 2002.

* indicates original appearance(s) of problem.

3 comments

Open Problem Garden

Bibliography

Reply

Navigate

Recent Activity