Home » Subject » Graph Theory » Basic G.T. » Cycles

Jones' conjecture

Importance: Medium ✭✭
Author(s): Kloks, Ton
Lee, Chuan-Min
Liu, Jiping
Subject: Graph Theory
» Basic Graph Theory
» » Cycles
Keywords: cycle packing
feedback vertex set
planar graph
Recomm. for undergrads: no
Posted by: cmlee
on: October 9th, 2007

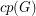For a graph $ G $, let $ cp(G) $ denote the cardinality of a maximum cycle packing (collection of vertex disjoint cycles) and let 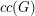$ cc(G) $ denote the cardinality of a minimum feedback vertex set (set of vertices 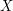$ X $ so that 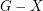$ G-X $ is acyclic).

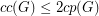Conjecture   For every planar graph $ G $, $ cc(G)\leq 2cp(G) $.

In [KLL], the authors mention that there exists a family of nonplanar graphs for which 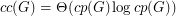$ cc(G) = \Theta( cp(G) \log cp(G) ) $, so no such result could hold for general graphs. They also point out that the conjecture is tight for wheels, and they prove it for the special case of outerplanar graphs.

Bibliography

*[KLL] Ton Kloks, Chuan-Min Lee, and Jiping Liu, New Algorithms for $ k $-Face Cover, $ k $-Feedback Vertex Set, and $ k $-Disjoint Cycles on Plane and Planar Graphs, in Proceedings of the 28th International Workshop on Graph-Theoretic Concepts in Computer Science (WG2002), LNCS 2573, pp. 282--295, 2002.


* indicates original appearance(s) of problem.
add new comment

Proved for subcubic planar

On December 5th, 2019 David Wood says:

Proved for subcubic planar graphs by Marthe Bonamy, François Dross, Tomáš Masařík, Wojciech Nadara, Marcin Pilipczuk, Michał Pilipczuk [https://arxiv.org/abs/1912.01570].

reply

Why Jones'?

On October 29th, 2007 Anonymous says:

Does anyone know why this is called Jones' Conjecture?

reply

Reply: Why Jones'?

On November 16th, 2007 Anonymous says:

I am Jones. My Taiwanese name is Chuan-Min Lee. This conjecture came up when I was working on it with Ton Kloks and Jiping Liu. I used the name "Jones" instead of my Taiwanese name for ease of communication.

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.