 login/create account
login/create account
Compatible Matching Conjecture (Solved)
For an even set  of points in the plane, a perfect matching of
of points in the plane, a perfect matching of  is a collection of nonintersecting segments such that every point of
is a collection of nonintersecting segments such that every point of  is an end of exactly one of the segments.
is an end of exactly one of the segments.
 be a set of points in the plane in general position such that
be a set of points in the plane in general position such that 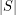 is divisible by 4. Then for every perfect matching
is divisible by 4. Then for every perfect matching  of
of  there is another perfect matching,
there is another perfect matching, 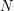 , of
, of  such that no segment of
such that no segment of  crosses a segment of
crosses a segment of 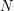 .
. More generally, we may say that two perfect matchings of  are compatible if their union is noncrossing, that is, it does not contain two (distinct) intersecting segments. (In contrary with what the conjecture demands, compatible matchings may share edges.)
are compatible if their union is noncrossing, that is, it does not contain two (distinct) intersecting segments. (In contrary with what the conjecture demands, compatible matchings may share edges.)
Motivation for the conjecture stems from the fact, that when we consider the graph with all perfect matchings of  as vertices, and edges connecting compatible matchings, then this graph is connected -- moreover it has diameter at most
as vertices, and edges connecting compatible matchings, then this graph is connected -- moreover it has diameter at most 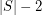 [1], and in fact at most
[1], and in fact at most 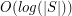 [2]. In [2] several stronger conjectures are proposed and it is shown, that for a matching
[2]. In [2] several stronger conjectures are proposed and it is shown, that for a matching  as in the conjecture, there is a matching
as in the conjecture, there is a matching 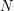 that does not intersect
that does not intersect  and
and 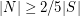 .
.
For some recent progress see [3, 4, 5].
(Apology to the authors of [2]: I suppose they all should be listed as authors of the conjecture, but the machine does not allow so many of them :-) Hopefully, this will be remedied soon.)
This conjecture has now been proved by Mashood Ishaque, Diane Souvaine and Csaba Toth [6].
Bibliography
[1] Michael E. Houle, Ferran Hurtado, Marc Noy, and Eduardo Rivera-Campo. Graphs of triangulations and perfect matchings. Graphs Combin., 21(3):325–331, 2005.
*[2] Oswin Aichholzer, Sergey Bereg, Adrian Dumitrescu, Alfredo García, Clemens Huemer, Ferran Hurtado, Mikio Kano, Alberto Márquez, David Rappaport, Shakhar Smorodinsky, Diane Souvaine, Jorge Urrutia, David R. Wood: Compatible geometric matchings, Computational Geometry: Theory and Applications, 42(6-7):617-626, 2009.
[3] Marwan Al-Jubeh, Michael Hoffmann, Mashhood Ishaque, Diane Souvaine and Csaba Toth. Convex Partitions with 2-Edge Connected Dual Graphs. 18th Fall Workshop on Computational Geometry, 2008.
[4] Nadia M. Benbernou, Erik D. Demaine, Martin L. Demaine, Michael Hoffmann, Mashhood Ishaque, Diane L. Souvaine, and Csaba D. Tóth, Disjoint Segments have Convex Partitions with 2-Edge Connected Dual Graphs. Proceedings of the 19th Canadian Conference on Computational Geometry (CCCG 2007), pages 13–16, 2007.
[5] Nadia Benbernou, Erik D. Demaine, Martin L. Demaine, Michael Hoffmann, Mashhood Ishaque, Diane Souvaine, and Csaba Toth. Erratum for "Disjoint segments have convex partitions with 2-edge connected dual graphs''. Proceedings of the 20th Canadian Conference on Computational Geometry (CCCG 2008), pages 223-226, 2008.
[6] Mashood Ishaque, Diane Souvaine and Csaba Toth. Disjoint Compatible Geometric Matchings. Proc. 27th Annual Symposium on Computational Geometry (SoCG 2011).
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University