 login/create account
login/create account
Diagonal Ramsey numbers
Let  denote the
denote the 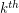 diagonal Ramsey number.
diagonal Ramsey number.
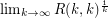 exists.
exists. Erdos offered $100 for a solution to the highlighted conjecture and $250 for a solution to the associated problem (these prizes are now provided by Graham).
Classic results of Erdos [E] and Erdos-Szekeres [ESz] give bounds on  which show that if
which show that if 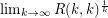 exists, then it is in the interval
exists, then it is in the interval ![$ [\sqrt{2},4] $](/files/tex/e60eefef54c8ed9f1796c217a67241a0e3ecd78e.png) . Although these arguments are quite basic, little progress has been made in improving these bounds. The best known lower bound on
. Although these arguments are quite basic, little progress has been made in improving these bounds. The best known lower bound on  is due to Spencer [S] and the best known upper bound is due to Thomason [T]. They are as follows:
is due to Spencer [S] and the best known upper bound is due to Thomason [T]. They are as follows: 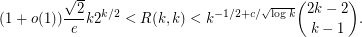
Gowers [G] has suggested that resolving these problems might require a rough structure theorem.
Bibliography
[E] P. Erdos, Some remarks on the theory of graphs, Bull. Amer. Math. Soc. 53 (1947), 292–294. MathSciNet
[ESz] P. Erdos and G. Szekeres, A combinatorial problem in geometry, Compositio Math. 2 (1935), 463–470.
[G] W. T. Gowers, Rough structure and classification, GAFA 2000 (Tel Aviv, 1999). Geom. Funct. Anal. 2000, Special Volume, Part I, 79--117. MathSciNet
[S] J. Spencer, Ramsey’s theorem—a new lower bound, J. Comb. Theory Ser. A 18 (1975), 108–115. MathSciNet
[T] A. Thomason, An upper bound for some Ramsey numbers, J. Graph Theory 12 (1988), 509–517. MathSciNet
* indicates original appearance(s) of problem.
Upper bound
The upper bound has been improved by David Conlon (to appear in Annals)

 Drupal
Drupal CSI of Charles University
CSI of Charles University
diagonal Ramsey numbers
Hi, My name is steve waterman.
re - diagonal Ramsey numbers
I have no proof of my conjectured formulas. However, the results are within the limits established in ALL cases. There is also a logic to these numbers as you will see.
http://www.watermanpolyhedron.com/RAMSEY.html
It is my belief that these values are indeed exact...that is, no bounds required, and thus an answer to this riddle - and as I also see it....only to be proven later. It is a big claim no doubt. I doubt that I will ever see a counter-example nor a single proof of say R(5,5) as long as I live. Lastly, knowing that these MAY INDEED BE the correct values...give us a chance to zero in upon these numbers specifically.
steve