 login/create account
login/create account
Funcoid corresponding to reloid through lattice Gamma (Solved)
Conjecture For every reloid 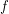 and
and 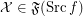 ,
, 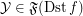 :
:
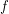 and
and 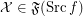 ,
, 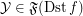 :
:- \item
![$ \mathcal{X} \mathrel{[(\mathsf{FCD}) f]} \mathcal{Y} \Leftrightarrow \forall F \in \operatorname{up}^{\Gamma (\operatorname{Src} f ; \operatorname{Dst} f)} f : \mathcal{X} \mathrel{[F]} \mathcal{Y} $](/files/tex/2f0c7dbaa1a5747d9bca753501374e8cd2500318.png) ; \item
; \item  .
. It's proved by me in this online article.
It's used notation from Algebraic General Topology draft book, modified by this note about new notation for a future version of this book.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University