 login/create account
login/create account
Hitting every large maximal clique with a stable set (Solved)
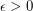 such that every graph contains a stable set which intersects every maximal clique of size
such that every graph contains a stable set which intersects every maximal clique of size  .
.
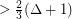 .
. Both forms of the conjecture are false, as shown by the following counterexample.
Take sufficiently large integers  and
and  , and let
, and let  be disjoint
be disjoint  -cliques, such that their union is a clique of size
-cliques, such that their union is a clique of size 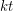 . Now add
. Now add 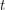 disjoint copies of
disjoint copies of 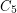 , labelled
, labelled 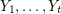 , with no edges between them and such that
, with no edges between them and such that 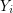 is complete to
is complete to  if
if 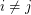 and anticomplete otherwise.
and anticomplete otherwise.
This graph has 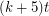 vertices and maximum degree
vertices and maximum degree 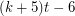 . Every edge in
. Every edge in 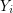 is in a maximal clique of size
is in a maximal clique of size 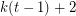 . It is straightforward to show that for every
. It is straightforward to show that for every 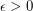 we can choose
we can choose  and
and 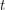 sufficiently large that this graph is a counterexample.
sufficiently large that this graph is a counterexample.
The original discussion of the conjecture follows.
King [K] proved that any graph  with
with 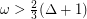 contains a stable set intersecting every maximum clique. This used the same approach as Rabern's earlier proof for graphs with
contains a stable set intersecting every maximum clique. This used the same approach as Rabern's earlier proof for graphs with 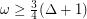 , but exploited a more general existence condition for independent systems of representatives.
, but exploited a more general existence condition for independent systems of representatives.
One of the key lemmas is Hajnal's clique collection lemma, which states that for any collection of maximum cliques in a graph, the sum of the intersection and the union is at least 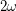 . Unfortunately the same result does not hold when restricted to large maximal cliques. Thus the case of maximal cliques would require a different approach.
. Unfortunately the same result does not hold when restricted to large maximal cliques. Thus the case of maximal cliques would require a different approach.
This conjecture is motivated by a local strengthening of Reed's omega, Delta, chi conjecture.
Bibliography
[K] Andrew D. King. Hitting all maximum cliques with a stable set using lopsided independent transversals, J. Graph Theory, n/a, doi: 10.1002/jgt.20532.
[R] Landon Rabern. On hitting all maximum cliques with an independent set, J. Graph Theory, 66 (2010), 32--37, doi: 10.1002/jgt.20487.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University