Home » Subject » Graph Theory

Stable set meeting all longest directed paths.

Importance: Medium ✭✭
Author(s): Laborde, Jean-Marie
Payan, Charles
Xuong N.H.
Subject: Graph Theory
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: March 1st, 2013
Conjecture   Every digraph has a stable set meeting all longest directed paths

If the stability number is 1, that is if the digraph is a tournament, it follows Redei's Theorem stating that every tournament has a directed hamiltonian path. The conjecture has been proved by Havet [H] for digraphs having stability number 2.

The conjecture would give an easy inductive proof of Gallai-Roy Theorem: every digraph with chromatic number $ k $ contains a directed path on $ k $ vertices.

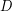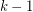Hahn and Jackson [HJ] conjectured that in contrast there is no directed path meeting every maximum stable set. In fact, they conjectured the following: For each positive integer $ k $, there is a digraph $ D $ with stability number $ k $ such that deleting the vertices of any $ k-1 $ directed paths in 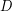$ D $ leaves a digraph with stability number $ k $. This was proved by Fox and Sudakov [FS] by a probabilistic argument.

Bibliography

[FS] J. Fox and B. Sudakov, Paths and stability number in digraphs, Electronic Journal of Combiantorics, 16 (2009), no.1, N23.

[HJ] G. Hahn and B. Jackson, A note concerning paths and independence number in digraphs, Discrete Math. 82 (1990), 327–329.

[H] F. Havet. Stable set meeting every longest path. Discrete Mathematics, 289 (2004), no. 1-3, 169-173.

*[LPX] J.M. Laborde, C. Payan, and N.H. Xuong, Independent sets and longest directed paths in digraphs. In Graphs and other Combinatorial Topics (Prague, 1982)}, Teubner-Texte Math., Vol. 59 (1983), 173-177, Teubner, Leipzig.


* indicates original appearance(s) of problem.
add new comment