 login/create account
login/create account
What is the smallest number of disjoint spanning trees made a graph Hamiltonian
We are given a complete simple undirected weighted graph 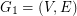 and its first arbitrary shortest spanning tree
and its first arbitrary shortest spanning tree 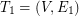 . We define the next graph
. We define the next graph 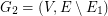 and find on
and find on 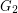 the second arbitrary shortest spanning tree
the second arbitrary shortest spanning tree 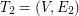 . We continue similarly by finding
. We continue similarly by finding  on
on 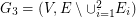 , etc. Let k be the smallest number of disjoint shortest spanning trees as defined above and let
, etc. Let k be the smallest number of disjoint shortest spanning trees as defined above and let 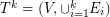 be the graph obtained as union of all
be the graph obtained as union of all  disjoint trees.
disjoint trees.
Question 1. What is the smallest number of disjoint spanning trees creates a graph 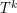 containing a Hamiltonian path.
containing a Hamiltonian path.
Question 2. What is the smallest number of disjoint spanning trees creates a graph 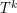 containing a shortest Hamiltonian path?
containing a shortest Hamiltonian path?
Questions 3 and 4. Replace in questions 1 and 2 a shortest spanning tree by a 1-tree. What is the smallest number of disjoint 1-trees creates a Hamiltonian graph? What is the smallest number of disjoint 1-trees creates a graph containing a shortest Hamiltonian cycle?
These questions are induced by the following paper Chrobak and Poljak. On common edges in optimal solutions to travelling salesman and other optimization problems, Discrete Applied Mathematics 20 (1988) 101-111.
Bibliography
M. Chrobak and S. Poljak. On common edges in optimal solutions to travelling salesman and other optimization problems, Discrete Applied Mathematics 20 (1988) 101-111.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Is this statement correct?
Unless I am mistaken, it appears that there does not exist any for which any of the above problems has a positive solution. For instance, let
for which any of the above problems has a positive solution. For instance, let  be the complete graph with vertex set
be the complete graph with vertex set 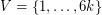 , and define
, and define 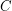 to be the edge-cut of
to be the edge-cut of  consisting of all edges between
consisting of all edges between  and
and  . Now define a weighting of
. Now define a weighting of  by assigning each edge in
by assigning each edge in 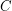 weight 1 and every other edge weight 2. So, the subgraph
weight 1 and every other edge weight 2. So, the subgraph 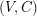 (consisting of all edges of weight 1) is isomorphic to
(consisting of all edges of weight 1) is isomorphic to 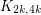 - and since
- and since 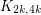 has
has  edge-disjoint spanning trees (by the Nash-Williams theorem, say), our procedure may well choose trees
edge-disjoint spanning trees (by the Nash-Williams theorem, say), our procedure may well choose trees 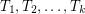 so that all of the edges in all of these graphs are in
so that all of the edges in all of these graphs are in 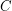 . But then
. But then  will not have a Hamiltonian path since it is a subgraph of
will not have a Hamiltonian path since it is a subgraph of 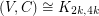 .
.
Of course, we may modify the edge weights here so that the procedure is forced to choose so that all of these trees have their edges in
so that all of these trees have their edges in 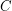 .
.