 login/create account
login/create account
Woodall's Conjecture
 is a directed graph with smallest directed cut of size
is a directed graph with smallest directed cut of size  , then
, then  has
has  disjoint dijoins.
disjoint dijoins. Definitions: Let  be a directed graph. A directed cut of
be a directed graph. A directed cut of  is an edge-cut in which all edges are directed the same way. A dijoin is a set of edges which intersect every directed cut.
is an edge-cut in which all edges are directed the same way. A dijoin is a set of edges which intersect every directed cut.
There is an important theorem of Lucchesi and Younger [LY] which asserts that the dual problem has an optimum integer packing. That is, for every digraph  in which the smallest dijoin has size
in which the smallest dijoin has size  , there exist
, there exist  pairwise disjoint directed cuts. This result implies more generally (in the terminology of Corneujols [C]) that the clutter of (minimal) directed cuts has the max-flow min-cut property (MFMC). It follows from this and Lehman's theorem [L] that the clutter of (minimal) dijoins is ideal. Therefore, if the smallest directed cut of
pairwise disjoint directed cuts. This result implies more generally (in the terminology of Corneujols [C]) that the clutter of (minimal) directed cuts has the max-flow min-cut property (MFMC). It follows from this and Lehman's theorem [L] that the clutter of (minimal) dijoins is ideal. Therefore, if the smallest directed cut of  has size
has size  , then there exist nonnegative rational numbers
, then there exist nonnegative rational numbers 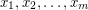 summing to
summing to  and dijoins
and dijoins 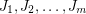 so that if each dijoin
so that if each dijoin 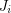 is taken with weight
is taken with weight 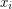 , the total weight of the dijoins containing any edge is at most 1. The above conjecture asserts that such a combination exists with
, the total weight of the dijoins containing any edge is at most 1. The above conjecture asserts that such a combination exists with 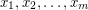 integral.
integral.
Schrijver [Sc80] has found a digraph in which the clutter of (minimal) dijoins does not have the MFMC property. Thus, the weighted version of Woodall's conjecture is not true in general. However, this clutter does have the MFMC property in a number of interesting special cases. One such example (due to Schrijver [Sc82] and Feofiloff, Younger [FY]) is when the digraph is acyclic and every source is joined to every sink by a directed path. Since every such digraph has the MFMC property, every such digraph must satisfy Woodall's conjecture.
There seem to be few positive results towards Woodall's conjecture for general digraphs. Although this was probably already known, Seymour and I (M. DeVos) observed that the conjecture is true for 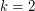 . To see this, note that the underlying graph is 2-edge-connected, so it may be oriented to give a strongly connected digraph, call it
. To see this, note that the underlying graph is 2-edge-connected, so it may be oriented to give a strongly connected digraph, call it  . Now partition the edges into two sets
. Now partition the edges into two sets 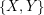 where
where 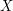 consists of those edges which have the same orientation in both
consists of those edges which have the same orientation in both  and
and  , and
, and 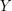 consists of those edges with different orientations in the two graphs. It is immediate that both
consists of those edges with different orientations in the two graphs. It is immediate that both 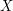 and
and 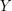 meet every directed cut, so each is a dijoin. Extending this to
meet every directed cut, so each is a dijoin. Extending this to 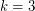 appears difficult. Indeed, I believe the following weak version of this is still open.
appears difficult. Indeed, I believe the following weak version of this is still open.
 so that every digraph with all directed cuts of size
so that every digraph with all directed cuts of size 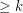 contains three pairwise disjoint dijoins.
contains three pairwise disjoint dijoins. The restriction of this conjecture to the special case of planar graphs is also open. Here we can use duality to restate the conjecture. Call a set of edges  a feedback arc-set if
a feedback arc-set if  intersects every directed cycle (or equivalently,
intersects every directed cycle (or equivalently, 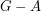 is acyclic).
is acyclic).
 is a planar digraph with all directed cycles of length
is a planar digraph with all directed cycles of length 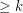 , then
, then  contains
contains  pairwise disjoint feedback arc-sets.
pairwise disjoint feedback arc-sets. The above conjecture is known to fail when the assumption of planarity is removed. On the other hand, it does hold for digraphs which are orientations of series-parallel graphs [LW]. It is also still open for 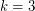 .
.
Bibliography
[C] G. Cornuejols, Combinatorial Optimization, Packing and Covering SIAM, Philadelphia (2001). MathSciNet
[FY] P. Feofiloff and D. H. Younger, Directed cut transversal packing for source-sink connected graphs. Combinatorica 7 (1987), no. 3, 255--263. MathSciNet
[LW] O. Lee, Y. Wakabayashi, Note on a min-max conjecture of Woodall. J. Graph Theory 38 (2001), no. 1, 36--41. MathSciNet
[LY] C.L. Lucchesi and D. H. Younger A minimax theorem for directed graphs, Journal of the London Math. Soc. (2) 17 (1978) 369-374. MathSciNet
[Sc80] A. Schrijver, A counterexample to a conjecture of Edmonds and Giles, Discrete Math. 32 (1980) 213-214. MathSciNet
[Sc82] A. Schrijver, Min-max relations for directed graphs, Annals of Discrete Math. 16 (1982) 261-280. MathSciNet
[W] D. R. Woodall, Menger and König systems. Theory and applications of graphs (Proc. Internat. Conf., Western Mich. Univ., Kalamazoo, Mich., 1976), pp. 620--635, Lecture Notes in Math., 642, Springer, Berlin, 1978. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University