 login/create account
login/create account
Sum-product problem
For every 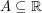 we let
we let 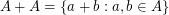 and
and  .
.
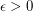 , every sufficiently large finite set
, every sufficiently large finite set 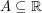 satisfies
satisfies ![\[ \max \{ |A \cdot A|, |A + A| \} \ge |A|^{2 - \epsilon} \]](/files/tex/de862bc1660fe79e0bc0067ee21dd3805bbbad82.png)
This famous conjecture asserts that every set of numbers  must have either a large sumset (
must have either a large sumset (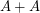 ) or a large product set (
) or a large product set (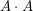 ). It is central to our understanding of the interplay between the additive and multiplicative properties of a set of numbers. Although this problem was originally posed just for subsets of integers, it is generally believed to hold true more generally for the reals.
). It is central to our understanding of the interplay between the additive and multiplicative properties of a set of numbers. Although this problem was originally posed just for subsets of integers, it is generally believed to hold true more generally for the reals.
It is relatively easy to show that every set 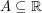 satisfies
satisfies 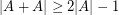 (use the order on
(use the order on 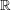 ). Furthermore, the sets
). Furthermore, the sets  which meet this lower bound are precisely the arithmetic progressions. A famous (and very useful) theorem of Freiman gives a rough generalization of this. He proves that for every fixed constant
which meet this lower bound are precisely the arithmetic progressions. A famous (and very useful) theorem of Freiman gives a rough generalization of this. He proves that for every fixed constant  , every set
, every set  with
with  is efficiently contained in a generalized arithmetic progression. Arithmetic progressions, and more generally the type of sets which appear in Freiman's theorem have large product sets, so they would obey this conjecture. Similarly, to minimize
is efficiently contained in a generalized arithmetic progression. Arithmetic progressions, and more generally the type of sets which appear in Freiman's theorem have large product sets, so they would obey this conjecture. Similarly, to minimize 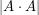 we should choose
we should choose  to be a geometric progression, and there is a similar structure theorem for when
to be a geometric progression, and there is a similar structure theorem for when 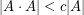 which would imply, in particular, that such sets have
which would imply, in particular, that such sets have 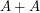 very large. So, in short, when either
very large. So, in short, when either 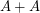 or
or 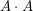 is very small, we have structure theorems which prove that the other is very large. Unfortunately, we have only rather weak information about sets
is very small, we have structure theorems which prove that the other is very large. Unfortunately, we have only rather weak information about sets  when both
when both 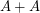 and
and 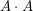 are somewhat larger.
are somewhat larger.
Erdos and Szemeredi were the first to prove that there exists 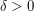 so that
so that  for all sufficiently large sets
for all sufficiently large sets  . This parameter
. This parameter  has been steadily improved by a number of authors. One highlight in this sequence is a proof by Elekes that
has been steadily improved by a number of authors. One highlight in this sequence is a proof by Elekes that  may be taken arbitrarily close to
may be taken arbitrarily close to 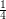 . His argument utilizes a clever application of the Szemeredi-Trotter theorem on point-line incidences and is described in detail on Terry Tao's blog. Very recently, Solymosi [S] found a simple and beautiful proof which shows that
. His argument utilizes a clever application of the Szemeredi-Trotter theorem on point-line incidences and is described in detail on Terry Tao's blog. Very recently, Solymosi [S] found a simple and beautiful proof which shows that  may be taken arbitrarily close to
may be taken arbitrarily close to 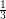 . An easily-digested simplification of his argument appears on Izabella Laba's blog.
. An easily-digested simplification of his argument appears on Izabella Laba's blog.
Bibliography
[S] J. Solymosi, An upper bound on the multiplicative energy.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University