 login/create account
login/create account
Schrijver, Alexander
Bases of many weights ★★★
Let  be an (additive) abelian group, and for every
be an (additive) abelian group, and for every 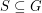 let
let 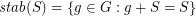 .
.
Conjecture Let 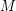 be a matroid on
be a matroid on  , let
, let 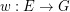 be a map, put
be a map, put 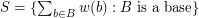 and
and 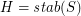 . Then
. Then 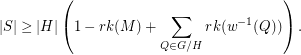
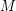 be a matroid on
be a matroid on  , let
, let 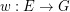 be a map, put
be a map, put 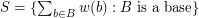 and
and 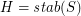 . Then
. Then 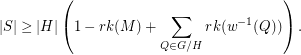

 Drupal
Drupal CSI of Charles University
CSI of Charles University