 login/create account
login/create account
Bases of many weights
Let  be an (additive) abelian group, and for every
be an (additive) abelian group, and for every 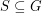 let
let  .
.
 be a matroid on
be a matroid on 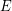 , let
, let 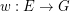 be a map, put
be a map, put 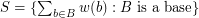 and
and 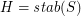 . Then
. Then 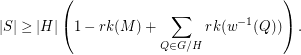
Although this conjecture may look a bit technical, it is in fact very natural, and important.
There is an interesting branch of combinatorial number theory which begins with the Cauchy-Davenport theorem, and M. Kneser's generelization of this theorem. We highlight these two theorems below. For a positive integer  , we let
, we let 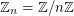 .
.
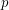 is prime and
is prime and 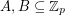 are nonempty, then
are nonempty, then 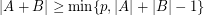 .
.  be finite and nonempty, and let
be finite and nonempty, and let  . Then
. Then 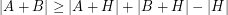 .
. In a somewhat underappreciated paper of Schrijver and Seymour, they find a generalization of the Cauchy-Davenport theorem to matroids. Namely, they prove the following.
 be a matroid on
be a matroid on 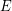 , let
, let 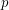 be prime, and let
be prime, and let 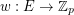 be a map. Then
be a map. Then 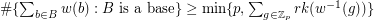 .
. The special case of this theorem when the underlying matroid is obtained from the free matroid on two elements by adding parallel edges is exactly the Cauchy-Davenport theorem. Further, their conjecture is precisely the common generalization of their theorem and Kneser's theorem.
DeVos, Goddyn, and Mohar have proved this conjecture in the special case when the underlying matroid is obtained from a uniform matroid by adding parallel elements, but apart from that, little is known.
Bibliography
[C] A.L. Cauchy, Recherches sur les nombers, J. Ecole Polytechniques, 9 (1813), 99-123.
[D] H. Davenport, On the addition of residue classes, J. London Math. Soc., 10 (1935), 30-32.
[K] M. Kneser, Abschätzung der aymptotischen dichte von summenmengen, Math. Z. (1953) 459-484.
[N] M.B. Nathanson, Additive Number Theory, GTM 165, Springer, 1996.
*[SS] A. Schrijver and P.D. Seymour, Spanning trees of different weights. Polyhedral combinatorics, DIMACS Ser. Discrete Math. Theoret. Comp. Sci., 1, 281-288.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University