 login/create account
login/create account
 with no bridge, there exist three disjoint sets
with no bridge, there exist three disjoint sets 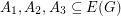 with
with 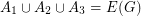 so that
so that  has a nowhere-zero 4-flow for
has a nowhere-zero 4-flow for  .
. A graph  has a nowhere-zero 4-flow if and only if there exist disjoint sets
has a nowhere-zero 4-flow if and only if there exist disjoint sets 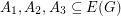 with
with 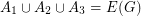 so that
so that  has a nowhere-zero 2-flow for
has a nowhere-zero 2-flow for  . Thus, the above conjecture is true with room to spare for such graphs. Since every 4-edge-connected graph and every 3-edge-colorable cubic graph has a nowhere-zero 4-flow, this conjecture is automatically true for these families. As with the 5-flow conjecture or the cycle double cover conjecture, establishing this conjecture comes down to proving it for cubic graphs which are not 3-edge-colorable.
. Thus, the above conjecture is true with room to spare for such graphs. Since every 4-edge-connected graph and every 3-edge-colorable cubic graph has a nowhere-zero 4-flow, this conjecture is automatically true for these families. As with the 5-flow conjecture or the cycle double cover conjecture, establishing this conjecture comes down to proving it for cubic graphs which are not 3-edge-colorable.
This conjecture is a consequence of the Petersen coloring conjecture, and it implies the Orientable cycle four cover conjecture. The latter implication follows immediately from the fact that every graph with a nowhere-zero 4-flow has an orientable cycle double cover. Actually, it is possible that for every graph  with no cut-edge, there exist disjoint sets
with no cut-edge, there exist disjoint sets 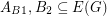 with
with  and so that
and so that 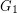 and
and 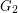 have nowhere-zero 3-flows and
have nowhere-zero 3-flows and 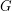 has a nowhere-zero 2-flow. The Petersen graph has such a decomposition (
has a nowhere-zero 2-flow. The Petersen graph has such a decomposition (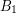 and
and 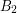 should be alternate edges of some 8-circuit) and so does every graph with a nowhere-zero 4-flow. If this stronger statement is true, then it would imply the oriented eight cycle four cover conjecture.
should be alternate edges of some 8-circuit) and so does every graph with a nowhere-zero 4-flow. If this stronger statement is true, then it would imply the oriented eight cycle four cover conjecture.
Bibliography
[J] F. Jaeger, On circular flows in graphs. Finite and infinite sets, Vol. I, II (Eger, 1981), 391--402, Colloq. Math. Soc. János Bolyai, 37, North-Holland, Amsterdam, 1984.. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University