 login/create account
login/create account
 (probably
(probably 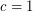 suffices) so that every graft with minimum
suffices) so that every graft with minimum  -cut size at least
-cut size at least  contains a
contains a  -join packing of size at least
-join packing of size at least  .
. Definitions: A graft consists of a graph 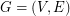 together with a distinguished set
together with a distinguished set 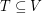 of even cardinality. A
of even cardinality. A  -cut is an edge-cut
-cut is an edge-cut 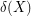 of
of  with the property that
with the property that 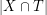 is odd. A
is odd. A  -join is a set
-join is a set 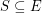 with the property that a vertex of
with the property that a vertex of 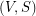 has odd degree if and only if it is in
has odd degree if and only if it is in  . A
. A  -join packing is a set of pairwise disjoint T-joins.
-join packing is a set of pairwise disjoint T-joins.
It is an easy fact that every  -join and every
-join and every  -cut intersect in an odd number of elements. It follows easily from this that the maximum size of a
-cut intersect in an odd number of elements. It follows easily from this that the maximum size of a  -join packing is always less than or equal to the minimum size of a
-join packing is always less than or equal to the minimum size of a  -cut. There is a simple example of a graft with
-cut. There is a simple example of a graft with 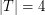 with minimum
with minimum  -cut size
-cut size  which contains only
which contains only 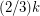 disjoint T-joins. The above conjecture asserts that this is essentially the worst case. DeVos and Seymour [DS] have obtained a partial result toward the above conjecture, proving that every graft with minimum
disjoint T-joins. The above conjecture asserts that this is essentially the worst case. DeVos and Seymour [DS] have obtained a partial result toward the above conjecture, proving that every graft with minimum  -cut size
-cut size  contains a
contains a  -join packing of size at least the floor of
-join packing of size at least the floor of 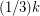 .
.
Definition: We say that a graft  is an
is an  -graph if
-graph if  is
is  -regular,
-regular, 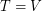 , and every
, and every  -cut of G has size at least
-cut of G has size at least  .
.
 is an
is an  -graph, then
-graph, then  contains a
contains a  -join packing of size at least
-join packing of size at least  .
. In an  -graph, every perfect matching is a
-graph, every perfect matching is a  -join, so the above conjecture is true with room to spare for
-join, so the above conjecture is true with room to spare for  -graphs which are
-graphs which are  -edge-colorable. Indeed, Seymour had earlier conjectured that every
-edge-colorable. Indeed, Seymour had earlier conjectured that every  -graph contains
-graph contains  disjoint perfect matchings. This however was disproved by Rizzi [R] who constructed for every
disjoint perfect matchings. This however was disproved by Rizzi [R] who constructed for every 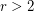 an
an  -graph in which every two perfect matchings intersect. Rizzi suggested the above problem as a possible fix for Seymour's conjecture. DeVos and Seymour have proved that every
-graph in which every two perfect matchings intersect. Rizzi suggested the above problem as a possible fix for Seymour's conjecture. DeVos and Seymour have proved that every  -graph has a
-graph has a  -join packing of size at least the floor of
-join packing of size at least the floor of 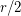 .
.
Definition: Let  be a graph and let
be a graph and let  be the set of vertices of
be the set of vertices of  of odd degree. A
of odd degree. A  -join of
-join of 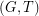 is defined to be a postman set.
is defined to be a postman set.
Note that when  is the set of vertices of odd degree, a cocycle of
is the set of vertices of odd degree, a cocycle of  is a
is a  -cut if and only if it has odd size. Rizzi has shown that the following conjecture is equivalent to the above conjecture in the special case when
-cut if and only if it has odd size. Rizzi has shown that the following conjecture is equivalent to the above conjecture in the special case when  is odd.
is odd.
 has size
has size 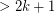 then the edges of
then the edges of  may be partitioned into
may be partitioned into 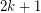 postman sets.
postman sets. The Petersen graph (or more generally any non  -edge-colorable
-edge-colorable  -graph) shows that the above conjecture would be false with the weaker assumption that every odd edge-cut has size
-graph) shows that the above conjecture would be false with the weaker assumption that every odd edge-cut has size 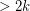 . The following conjecture asserts that odd edge-cut size
. The following conjecture asserts that odd edge-cut size 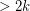 is enough (for the same conclusion) if we assume in addition that G has no Petersen minor.
is enough (for the same conclusion) if we assume in addition that G has no Petersen minor.
 has no Petersen minor and every odd edge-cut of
has no Petersen minor and every odd edge-cut of  has size
has size 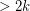 then the edges of
then the edges of  may be partitioned into
may be partitioned into 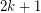 postman sets.
postman sets. Gerard Cornuejols [C] has kindly offered $5000 for a solution to this conjecture. However, it will be tough to find a quick proof since this conjecture does imply the 4-color theorem. Robertson, Seymour, Sanders, and Thomas [RSST] have proved the above conjecture for cubic graphs. Conforti and Johnson [CJ] proved it under the added hypothesis that G has no 4-wheel minor.
Bibliography
[CJ] M. Conforti and E.L. Johnson, Two min-max theorems for graphs noncontractible to a four wheel, preprint.
[C] G. Cornuejols, Combinatorial Optimization, packing and covering, SIAM, Philadelphia (2001).
[R] R. Rizzi, Indecomposable r-Graphs and Some Other Counterexamples, J. Graph Theory 32 (1999) 1-15. MathSciNet
[RSST] N. Robertson, D.P. Sanders, P.D. Seymour, and R. Thomas, A New Proof of the Four-Color Theorem, Electron. Res. Announc., Am. Math. Soc. 02, no 1 (1996) 17-25.
[S] P.D. Seymour, Some Unsolved Problems on One-Factorizations of Graphs, in Graph Theory and Related Topics, edited by J.A. Bondy and U.S.R. Murty, Academic Press, New York 1979) 367-368.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University