Home » Subject » Graph Theory » Coloring » Edge coloring
Importance: Medium ✭✭
Author(s): Fiamcik, Jozef
Subject: Graph Theory
» Coloring
» » Edge coloring
Keywords: edge-coloring
Recomm. for undergrads: no
Prize: none
Posted by: mdevos
on: March 7th, 2007
Conjecture   Every simple graph with maximum degree $ \Delta $ has a proper $ (\Delta+2) $-edge-colouring so that every cycle contains edges of at least three distinct colours.

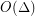An edge-colouring with the property that every cycle contains edges of at least three distinct colours is called an acyclic edge-colouring. It is known (see [AMR]) that every graph of maximum degree $ \Delta $ has an acyclic edge-colouring of size $ O(\Delta ) $. The best upper bound so far is 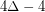$ 4\Delta -4 $ and is due to Esperet and Parreau [EP]. It is also known (see [ASZ]) that this conjecture is true for graphs with girth at least 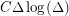$ C \Delta \log(\Delta ) $ (for some fixed constant $ C $).

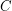Bibliography

[AMR] N. Alon, C. McDiarmid and B. Reed, Acyclic colouring of graphs, Random Structures and Algorithms 2 (1991), 277-288. MathSciNet

[ASZ] N. Alon, B. Sudakov and A. Zaks, Acyclic edge-colorings of graphs, J. Graph Theory 37 (2001), 157-167. MathSciNet

[EP] L. Esperet and A. Parreau, Acyclic edge-coloring using entropy compression, arXiv:1206.1535 [math.CO].


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options