 login/create account
login/create account
Let 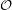 denote the graph with vertex set consisting of all lines through the origin in
denote the graph with vertex set consisting of all lines through the origin in 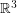 and two vertices adjacent in
and two vertices adjacent in 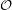 if they are perpendicular.
if they are perpendicular.
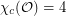 ?
? In the problem statement,  denotes the circular chromatic number.
denotes the circular chromatic number.
Coloring properties of 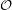 are, rather surprisingly, of interest in quantum mechanics. If the spins of certain particles are measured in three orthogonal directions, then these measurements always return one
are, rather surprisingly, of interest in quantum mechanics. If the spins of certain particles are measured in three orthogonal directions, then these measurements always return one  and two values which are
and two values which are  . If such a particle has "decided" in advance how it will respond to any possible measurement, then the set of directions in which it will respond
. If such a particle has "decided" in advance how it will respond to any possible measurement, then the set of directions in which it will respond  must be an independent set in the orthogonality graph
must be an independent set in the orthogonality graph 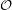 which meets every triangle. Kochen and Specker have shown that
which meets every triangle. Kochen and Specker have shown that 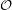 (even certain finite subgraphs of it) does not have any independent set meeting every triangle, thus exhibiting a rather mysterious property of these particles. In some sense, if the person doing the measurement has the free will to decide in which directions to measure, then the particle must have some free will to decide how it will respond.
(even certain finite subgraphs of it) does not have any independent set meeting every triangle, thus exhibiting a rather mysterious property of these particles. In some sense, if the person doing the measurement has the free will to decide in which directions to measure, then the particle must have some free will to decide how it will respond.
The property that 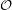 has no independent set which meets every triangle shows that
has no independent set which meets every triangle shows that 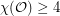 . On the other hand, if we center a regular octahedron at the origin, and assign a color to each line
. On the other hand, if we center a regular octahedron at the origin, and assign a color to each line 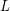 depending on which pair of opposite faces it passes through (if
depending on which pair of opposite faces it passes through (if 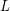 meets more than one pair of opposite faces, just choose one) we get a proper 4-coloring of
meets more than one pair of opposite faces, just choose one) we get a proper 4-coloring of 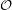 . Therefore,
. Therefore,  .
.
These bounds prove that  . By investigating certain finite subgraphs of
. By investigating certain finite subgraphs of 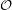 , DeVos, Ghebleh, Goddyn, Mohar, and Naserasr have shown that
, DeVos, Ghebleh, Goddyn, Mohar, and Naserasr have shown that 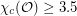 .
.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University