Open Problem Garden

Importance: Medium ✭✭

Author(s):

Subject:	Graph Theory
	» Coloring

Keywords:	degenerate
	girth

Recomm. for undergrads: yes

Posted	by:	David Wood
	on:	March 16th, 2014

Solved by:

A. V. Kostochka and J. Nesetril, Properties of Descartes' construction of triangle-free graphs with high chromatic number, Combin. Prob. Comput. 8 (1999), 467-472.

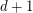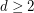Question Does there exist a $d$ -degenerate graph with chromatic number $d + 1$ and girth $g$ , for all $d \geq 2$ and $g \geq 3$ ?

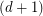A graph is $d$ -degenerate if every subgraph has a vertex of degree at most $d$ . Such graphs are $(d+1)$ -colourable by a minimum-degree-greedy algorithm. This bound is tight for complete graphs. More interestingly, Alon-Krivelevich-Sudakov [AKS] proved that it is tight for triangle-free graphs. That is, there are $d$ -degenerate triangle-free graphs with chromatic number 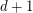$d + 1$ . Thus the answer to the above question is `yes' for 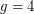$g=4$ . 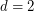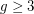Odd cycles show that the answer is `yes' for $d=2$ and $g\geq 3$ . 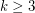A `yes' answer for $d\geq 2$ and $g\geq 4$ would generalise the famous result of Erdős [E], who proved that there are $k$ -chromatic graphs with girth $g$ for all $k\geq3$ and $g\geq 4$ . A `no' answer would also be interesting---this would provide a non-trivial upper bound on the chromatic number of $d$ -degenerate graphs with girth $g$ .