Open Problem Garden

A cubic graph is -edge-colorable for a Steiner triple system if its edges can be colored with the points of in such a way that the points assigned to three edges sharing a vertex form a triple in .

A Steiner triple system is called universal if any (simple) cubic graph is -colorable.

It is easy to see that if 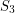denotes the trivial Steiner triple system with three points and one triple, then 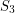-colorable graphs are precisely (cubic) edge-3-colorable graphs. For the same reason, any cubic edge-3-colorable graph is -colorable for any Steiner triple system (with at least one edge). Thus, the study of -colorings may be viewed as an attempt to understand snarks.

It is not hard to see, that a graph is Fano-colorable iff it has a nowhere-zero 8-flow. Thus (by Jaeger's result) Fano plane is "almost universal": it is possible to use it to color any bridgeless cubic graph (but it doesn't work for any graph with a bridge).

Grannell et al. [GGKS] constructed a universal Steiner triple system of order 381. Holroyd, Skoviera [HS] proved that neither projective nor affine Steiner triple systems are universal. Kral et al. [KMPS] proved that any non-affine non-projective non-trivial point-transitive Steiner triple system is universal.