 login/create account
login/create account
If  is a simple graph, we let
is a simple graph, we let 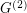 denote the simple graph with vertex set
denote the simple graph with vertex set 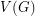 and two vertices adjacent if they are distance
and two vertices adjacent if they are distance 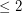 in
in  .
.
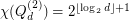 .
. Here  , denotes the
, denotes the  -dimensional hypercube, i.e. the graph with vertex set
-dimensional hypercube, i.e. the graph with vertex set 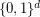 and two vertices adjacent if they differ in exactly one coordinate. So, the vertices with at most one coordinate equal to
and two vertices adjacent if they differ in exactly one coordinate. So, the vertices with at most one coordinate equal to 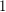 form a clique of size
form a clique of size 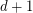 in
in  , giving us the easy lower bound
, giving us the easy lower bound 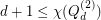 . An independent set in
. An independent set in  is precisely an error correcting code, so a proper coloring of this graph may be viewed as a covering of the hypercube with codes. Wan [W] constructed a coloring of
is precisely an error correcting code, so a proper coloring of this graph may be viewed as a covering of the hypercube with codes. Wan [W] constructed a coloring of  using
using  many colors, and he conjectures that this is optimal.
many colors, and he conjectures that this is optimal.
Note that  contains a subgraph isomorphic to
contains a subgraph isomorphic to  , so it suffices to prove the conjecture when
, so it suffices to prove the conjecture when  is a power of 2. The cases
is a power of 2. The cases  are rather easy to verify, but
are rather easy to verify, but 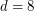 appears to be open.
appears to be open.
In his Ph.D. thesis, Ghebleh suggests the stronger conjecture that  has circular chromatic number equal to
has circular chromatic number equal to  .
.
Bibliography
[G] M. Ghebleh, Theorems and Computations in Circular Colourings of Graphs, Ph.D. thesis, Simon Fraser University, 2007.
*[W] P. J. Wan, Near-optimal conflict-free channel set assignments for an optical cluster-based hypercube network. J. Comb. Optim. 1 (1997), no. 2, 179--186. MathSciNet.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University