 login/create account
login/create account
4-flow conjecture
It is a consequence of a theorem of Tutte that a cubic graph has a nowhere-zero 4-flow if and only if it is 3-edge-colorable. Thus, the 4-flow conjecture implies that every bridgeless cubic graph with no Petersen minor is 3-edge-colorable (another conjecture of Tutte). Note that the Four Color Theorem is equivalent to the assertion that planar cubic graphs without bridges are 3-edge-colorable, so even this weaker conjecture is a strengthening of the Four Color Theorem. This weaker conjecture was recently proved by Robertson, Seymour, and Thomas [RST]. Their proof involves a reduction to the case of nearly planar graphs, and then an application of 4-color-theorem type techniques (computer assisted) to color these graphs.
Most conjectures about flows can be easily reduced to the case of cubic graphs by splitting arguments. The idea is to take a vertex  incident with edges
incident with edges 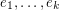 and "split"
and "split"  , that is, replace
, that is, replace  by two new vertices
by two new vertices 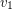 and
and 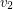 , and for every edge
, and for every edge 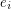 join it to either
join it to either 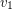 or
or 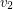 (sometimes the edge
(sometimes the edge 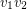 is also added). For instance, this technique can be used to reduce the general 5-flow conjecture down to the special case of cubic graphs. Unfortunately, that technique does not apply here, since splitting a vertex may introduce a Petersen minor.
is also added). For instance, this technique can be used to reduce the general 5-flow conjecture down to the special case of cubic graphs. Unfortunately, that technique does not apply here, since splitting a vertex may introduce a Petersen minor.
Petersen's graph is not an apex graph (deleting any vertex still leaves a nonplanar graph). It follows that no apex graph can have a Petersen minor, so the above conjecture implies that every bridgeless apex graph has a nowhere-zero 4-flow. By splitting the vertices which lie in the plane this can be reduced to the special case where all vertices which lie in the plane have degree 3. This is then equivalent to the following old conjecture of Gr\"{o}tzsch.
 is a 2-connected connected planar graph of maximum degree 3, then
is a 2-connected connected planar graph of maximum degree 3, then  is 3-edge-colorable unless it has exactly one vertex of degree 2.
is 3-edge-colorable unless it has exactly one vertex of degree 2. Bibliography
[AH] K. Appel, W. Haken, Every Planar Map is Four Colorable, Bull. Amer. Math. Soc. 82 (1976) 711-712. MathSciNet
[RSST] N. Robertson, D.P. Sanders, P.D. Seymour, and R. Thomas, A New Proof of the Four-Color Theorem, Electron. Res. Announc., Am. Math. Soc. 02, no 1 (1996) 17-25. MathSciNet
[RST] N. Robertson, P.D. Seymour, and R. Thomas, Tutte's edge-colouring conjecture. J. Combin. Theory Ser. B 70 (1997), no. 1, 166--183. MathSciNet
[Tut54] W.T. Tutte, A Contribution on the Theory of Chromatic Polynomials, Canad. J. Math. 6 (1954) 80-91. MathSciNet
[Tut66] W.T. Tutte, On the Algebraic Theory of Graph Colorings, J. Combinatorial Theory 1 (1966) 15-50. MathSciNet
* indicates original appearance(s) of problem.
What is wrong?
Perhaps you could elaborate.. what needs to be fixed?

 Drupal
Drupal CSI of Charles University
CSI of Charles University
fix the problm
fix the problm