 login/create account
login/create account
Cores of Cayley graphs
 be an abelian group. Is the core of a Cayley graph (on some power of
be an abelian group. Is the core of a Cayley graph (on some power of  ) a Cayley graph (on some power of
) a Cayley graph (on some power of  )?
)? Even the case 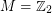 is open. In this case, Cayley graphs on some power of
is open. In this case, Cayley graphs on some power of  are called cube-like graphs, they have been introduced by Lov\'asz as an example of graphs, for which every eigenvalue is an integer.
are called cube-like graphs, they have been introduced by Lov\'asz as an example of graphs, for which every eigenvalue is an integer.
So, in this case we ask, whether a core of each cube-like graph is a cube-like graph.
Question needs refining...
As stated, the conjecture is false in an uninteresting way ... it is possible for a Cayley graph of Z_15 have a 5-cycle as a core.... So if we take M = Z_15 then the result is false.
Perhaps the question should either (a) be restricted to elementary abelian groups or (b) have the conclusion being that the core of a Cayley graph on M must be a Cayley graph on N where N is a (group) homomorphic image of M.
Gordon Royle http://people.csse.uwa.edu.au/gordon
Re: Question needs refining...
That is true. I was mainly thinking about 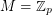 (for a prime
(for a prime 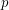 ). However, your suggestion (b) looks sensible as well.
). However, your suggestion (b) looks sensible as well.
Thanks for your comment!
Robert Samal

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Who first conjectured this?
Who first conjectured that the core of a cubelike graph is cubelike?