 login/create account
login/create account
Erdős-Posa property for long directed cycles
 be an integer. For every integer
be an integer. For every integer 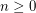 , there exists an integer
, there exists an integer 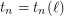 such that for every digraph
such that for every digraph  , either
, either  has a
has a  pairwise-disjoint directed cycles of length at least
pairwise-disjoint directed cycles of length at least 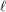 , or there exists a set
, or there exists a set  of at most
of at most 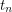 vertices such that
vertices such that 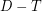 has no directed cycles of length at least
has no directed cycles of length at least 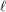 .
. The case  has been proved by Reed et al. [RRST], hence solving a conjecture of Gallai [G] and Younger [Y]. The case
has been proved by Reed et al. [RRST], hence solving a conjecture of Gallai [G] and Younger [Y]. The case  and
and  has previously been solved by McCuaig [M], who proved that
has previously been solved by McCuaig [M], who proved that 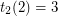 . Havet and Maia [HM] proved the case
. Havet and Maia [HM] proved the case  .
.
The analogous statement for undirected graph has been proved by Birmelé, Bondy and Reed [BBR], hence generalizing Erdős-Posa [EP] result for 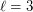 .
.
Bibliography
[BBR] E. Birmelé, J.A. Bondy, and B.A. Reed. The Erdos-Posa property for long circuits, Combinatorica, 27(2), 135–145, 2007.
[EP] P. Erdős and L. Pósa. On the independent circuits contained in a graph. Canad. J. Math., 17, 347--352, 1965.
[G] T. Gallai. Problem 6, in Theory of Graphs, Proc. Colloq. Tihany 1966 (New York), Academic Press, p.362, 1968.
*[HM] F. Havet and A. K. Maia. On disjoint directed cycles with prescribed minimum lengths. INRIA Research Report, RR-8286, 2013.
[M] W. McCuaig, Intercyclic digraphs. Graph Structure Theory, (Neil Robertson and Paul Seymour, eds.), AMS Contemporary Math., 147:203--245, 1993.
[RRST] B. Reed, N. Robertson, P.D. Seymour, and R. Thomas. Packing directed circuits. Combinatorica, 16(4):535--554, 1996.
[Y] D. H. Younger. Graphs with interlinked directed circuits. Proceedings of the Midwest Symposium on Circuit Theory, 2:XVI 2.1 - XVI 2.7, 1973.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University