 login/create account
login/create account
Good edge labeling and girth (Solved)
More specifically: there exists a constant  such that every graph with girth at least
such that every graph with girth at least  has a good edge labeling.
has a good edge labeling.
Let  be a finite undirected simple graph. A good edge labeling of
be a finite undirected simple graph. A good edge labeling of  is an assignment of distinct numbers to the edges such that every cycle has at least two local maxima. (The distinctness of the labels is required only to make the term `local maximum' unambiguous.)
is an assignment of distinct numbers to the edges such that every cycle has at least two local maxima. (The distinctness of the labels is required only to make the term `local maximum' unambiguous.)
Equivalently, a labeling of the edges is good, if for every pair of distinct vertices 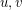 , there is at most one increasing path from
, there is at most one increasing path from  to
to  .
.
It is easy to verify that the graphs  and
and 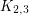 have no good edge labeling. In [ACGH2] an infinite class of graphs without good edge labelings is given. All these graphs have many 4-cycles.
have no good edge labeling. In [ACGH2] an infinite class of graphs without good edge labelings is given. All these graphs have many 4-cycles.
Indeed, no example is known of a graph of girth 5 or more without a good edge labeling. In other words, it may be possible that 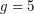 suffices for the conjecture.
suffices for the conjecture.
Bibliography
*[BFT] M. Bode, B. Farzad, D.O. Theis. Good edge-labelings and graphs with girth at least five.
[ACGH1] J. Araújo, N. Cohen, F. Giroire, F. Havet. Good edge-labelling of graphs. (English summary) LAGOS'09—V Latin-American Algorithms, Graphs and Optimization Symposium, 275–280, Electron. Notes Discrete Math., 35, Elsevier Sci. B. V., Amsterdam, 2009. MathSciNet
[ACGH2] J. Araujo, N. Cohen, F. Giroire, and F. Havet. Good edge-labelling of graphs. Research Report 6934, INRIA, 2009.
[BCP] J-C. Bermond, M. Cosnard, and S. Pérennes. Directed acyclic graphs with unique path property. Technical report 6932, INRIA, May 2009
* indicates original appearance(s) of problem.
link to the resolving paper
http://epubs.siam.org/doi/abs/10.1137/11085414X

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Solved
Mehrabian, SIAM J Discrete Math, 2012.