 login/create account
login/create account
The Two Color Conjecture
Conjecture If  is an orientation of a simple planar graph, then there is a partition of
is an orientation of a simple planar graph, then there is a partition of 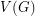 into
into  so that the graph induced by
so that the graph induced by  is acyclic for
is acyclic for 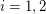 .
.
 is an orientation of a simple planar graph, then there is a partition of
is an orientation of a simple planar graph, then there is a partition of 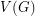 into
into  so that the graph induced by
so that the graph induced by  is acyclic for
is acyclic for 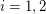 .
. This is a type of coloring digraphs introduced by V. Neumann-Lara. More generally, if  is a digraph, we wish to partition the vertex set of
is a digraph, we wish to partition the vertex set of  into as few parts as possible so that each induces an acyclic subgraph.
into as few parts as possible so that each induces an acyclic subgraph.
Bibliography
* [N] V. Neumann-Lara (1985). Vertex colourings in digraphs. Some problems. Technical report, University of Waterloo.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Riste Skrekovski conjectured
Riste Skrekovski conjectured at a graph theory meeting in Budmerice, Slovakia, in 2005 that this conjecture is false.