login/create account
Real roots of the flow polynomial
Conjecture All real roots of nonzero flow polynomials are at most 4.
For every graph 
, let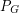 
be the chromatic polynomial of and let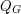 
be the flow polynomial of . If is loopless, then 
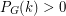for all sufficiently large integers 
(as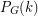 
= # of k-colorings of ). It follows from Seymour's 6-flow theorem that if has no bridge, then 
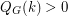for all integers 
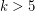(as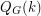 
= # of nowhere-zero flows in the group of integers modulo ). It is natural to ask if all real roots of these polynomials are small. For the chromatic polynomial, 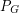, this is not the case. There exist graphs with chromatic number 3 for which 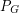has arbitrarily large real roots. The above conjecture asserts that the flow polynomial exhibits the opposite behavior. One word of caution, it is known that the set of roots of flow polynomials is dense in the complex plane.
Bibliography
[S] P.D. Seymour, Nowhere-Zero 6-Flows, J. Combinatorial Theory Ser. B 30 (1981) 130-135. MathSciNet
* indicates original appearance(s) of problem.
Welsh's conjecture is false
On August 21st, 2009 Gordon Royle says:
Welsh's conjecture on flow roots is false. In fact, many cubic graphs with reasonably large girth and enough vertices have flow roots between 4 and 5, and it is almost certain that we can find graphs with flow roots arbitrarily close to 5.
However I strongly believe that "All real roots of nonzero flow polynomials are at most FIVE".
See my recent survey article "Recent results on chromatic and flow roots of graphs and matroids, Surveys in Combinatorics 2009" for more detail.
Gordon Royle
Drupal
CSI of Charles University
Not bounded by 5, either
A preprint by Jesper L. Jacobsen and Jesus Salas claims that there are graphs with roots of their flow polynomial being above 5. The generalized Petersen graphs G(7n,7) are claimed to have roots of flow polynomial that accumulate at approximately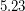
.
I suppose this makes the original conjecture truly false. An interesting variant, though, is to find out, if all roots of flow polynomials are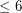
. (Thanks to Bojan Mohar for pointing out the paper to me.)