 login/create account
login/create account
Strong 5-cycle double cover conjecture
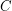 be a circuit in a bridgeless cubic graph
be a circuit in a bridgeless cubic graph  . Then there is a five cycle double cover of
. Then there is a five cycle double cover of  such that
such that 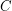 is a subgraph of one of these five cycles.
is a subgraph of one of these five cycles. A cycle in  is meant to be a
is meant to be a 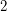 -regular subgraph of
-regular subgraph of  . A five cycle double cover of
. A five cycle double cover of  is a set of five cycles of
is a set of five cycles of  such that every edge of
such that every edge of  is contained in exactly two of these cycles.
is contained in exactly two of these cycles.
This conjecture is a combination and thus strengthening of the  -cycle double cover conjecture and the strong cycle double cover conjecture.
-cycle double cover conjecture and the strong cycle double cover conjecture.
Bibliography
* indicates original appearance(s) of problem.
Not a counterexample
Dear Nieke,
unfortunately, your graph is definitely not a counterexample. I could not follow your explanations, let me instead show, why your graph with the indicated cycle has the desired 5-CDC.
Your graph is planar, 2-edge-connected and the circuit C is a boundary of one of the faces. It turns out that for all such instances the conjecture is true: consider all face boundaries -- a collection of circuits. Now a proper 4-coloring of the dual graph splits the circuits into four cycles, the given circuit is contained in one of them. (The fifth cycle can be empty in this case.)
Think about it, and if you still believe you have a counterexample, post again. For now, I am not reading the other comments, as they prove something that turns out to be false :-).
Best wishes, Robert
Indeed, no counterexamples
Dear Robert,
Thanks for your reply.
I was thinking that the cycles have to be connected, which is obviously not true. So therefore my thought-to-be-counterexamples weren't correct. Thanks for the help! I wouldn't mind deleting all those comments, but I am not sure how to :)
Best, Nieke
Explanation of the 3-connected counterexample
Consider the circuit  to be color 1. And assume there is a 5-cycle cover containing this circuit as one of the cycles. We distinguish the cycles by color.
to be color 1. And assume there is a 5-cycle cover containing this circuit as one of the cycles. We distinguish the cycles by color.
Then 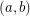 and
and 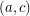 are colored with the same color (color 2) in the second cycle covering them, and similarly
are colored with the same color (color 2) in the second cycle covering them, and similarly 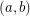 and
and 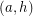 have the same color (color 3) in the second cycle covering them. (As otherwise
have the same color (color 3) in the second cycle covering them. (As otherwise 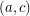 is colored twice by the cycle
is colored twice by the cycle 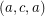 which, if allowed, quickly shows necessity of 6 colors)
which, if allowed, quickly shows necessity of 6 colors)
Explanation of the 3-connected counterexample (Part II)
Now 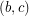 still needs to be covered twice, which cannot be done by 1 color as then again one needs 6 colors. One of the colors has to be color 2, otherwise this will leave
still needs to be covered twice, which cannot be done by 1 color as then again one needs 6 colors. One of the colors has to be color 2, otherwise this will leave  towards
towards  and
and  and therefore there will be no escape possibility from
and therefore there will be no escape possibility from  for the two new colors. So the triangle
for the two new colors. So the triangle 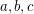 is colored with color 2. By symmetry the triangle
is colored with color 2. By symmetry the triangle 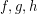 is also one color cycle (color 4). Now
is also one color cycle (color 4). Now 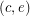 ,
, 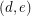 and
and 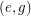 are not colored and therefore need to be in the cycle of color 3 and the cycle of color 5. But then
are not colored and therefore need to be in the cycle of color 3 and the cycle of color 5. But then  has degree 3 in both cycles which is a contradiction.
has degree 3 in both cycles which is a contradiction.
So a 5-cycle double cover containing this cycle does not exist.
?: Counterexample for a graph with a 2-cut
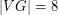
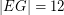
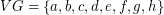
Adjacency matrix (in alphabetical order): ![\[ \left( \begin{array}{llllllll } 0&1&1&1&0&0&0&0 & 1&0&1&1&0&0&0&0 & 1&1&0&0&1&0&0&0 & 1&1&0&0&0&1&0&0 & 0&0&1&0&0&0&1&1 & 0&0&0&1&0&0&1&1 & 0&0&0&0&1&1&0&1 & 0&0&0&0&1&1&1&0 \end{array}\right)\]](/files/tex/7b6211a86e93145c2366fb71a06c85b3d54ea5ea.png)
Consider the circuit 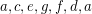 to be color 1, now on either side of the 2-cut, we need three more colors, of which only one color can serve both (due to the 2-cut), so we need at least 6 colors (6 cycles).
to be color 1, now on either side of the 2-cut, we need three more colors, of which only one color can serve both (due to the 2-cut), so we need at least 6 colors (6 cycles).
-----------
It could be so that I am making a mistake, if so, please explain my mistake to me.
I came to this point by simple trial and error.
I would like to upload a simple picture, but I seem to be a little lost on how to do this.
Nieke Aerts
Consider the circuit to be
Consider the circuit  to be color 1. And assume there is a 5-cycle cover containing this circuit as one of the cycles. We distinguish the cycles by color.
to be color 1. And assume there is a 5-cycle cover containing this circuit as one of the cycles. We distinguish the cycles by color.
Then 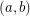 and
and 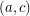 are colored with the same color (color 2) in the second cycle covering them, and similarly
are colored with the same color (color 2) in the second cycle covering them, and similarly 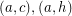 have the same color (color 3) in the second cycle covering them. (As otherwise
have the same color (color 3) in the second cycle covering them. (As otherwise 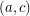 is colored twice by the cycle
is colored twice by the cycle 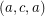 which, if allowed, quickly shows necessity of 6 colors)
which, if allowed, quickly shows necessity of 6 colors)
!!Ignore previous comment!!
Sorry, I pressed reply at the wrong statement.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
?: 3-connected Counterexample
Adjacency matrix (in alphabetical order):
For the explanation, see the following comment. -----------
It could be so that I am making a mistake, if so, please explain my mistake to me.
I came to this point by simple trial and error.
I would like to upload a simple picture, but I seem to be a little lost on how to do this.
Nieke Aerts