Home » Subject » Graph Theory » Directed Graphs

The Bermond-Thomassen Conjecture

Importance: Medium ✭✭
Author(s): Bermond, Jean-Claude
Thomassen, Carsten
Subject: Graph Theory
» Directed Graphs
Keywords: cycles
Recomm. for undergrads: no
Posted by: JS
on: October 1st, 2007
Conjecture   For every positive integer $ k $, every digraph with minimum out-degree at least $ 2k-1 $ contains $ k $ disjoint cycles.

This conjecture is a simple observation when 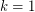$ k=1 $. It was proved by Thomassen~[Tho83] in 1983 when 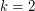$ k=2 $, and more recently the case 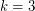$ k=3 $ was settled~[LPS07].

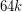The bound offered would be optimal — just consider a symmetric complete graph on $ 2k-1 $ vertices. In 1996, Alon~[Alo96] proved that the statement is true with $ 2k-1 $ replaced by $ 64k $. The conjecture was also verified for tournaments of minimum in-degree at least $ 2k-1 $~[BLS07].

Bang-Jensen et al. [BBT] made a stronger conjecture for digraph with sufficiently large girth.

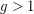Conjecture   For every integer $ g >1 $, every digraph 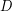$ D $ with girth at least 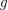$ g $ and with minimum out-degree at least 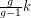$ \frac{g}{g-1}k $ contains $ k $ disjoint cycles.

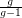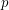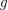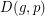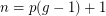The constant $ \frac{g}{g-1} $ is best possible. Indeed, for every integers $ p $ and $ g $, consider the digraph $ D(g,p) $ on $ n = p(g − 1) + 1 $ vertices with vertex set 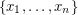$ \{x_1, \dots , x_n\} $ and arc set 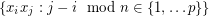$ \{x_ix_j : j − i \mod n \in \{1,\dots p\}\} $. It has girth 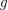$ g $ and out-degree 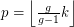$ p = \left \lfloor \frac{g}{g−1} k \right \rfloor $. Moreover, for 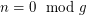$ n = 0 \mod g $, the digraph 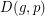$ D(g,p) $ admits a partition into $ k $ vertex disjoint 3-cycles and no more. For g = 3, the first case of this conjecture which differs from Bermond-Thomassen Conjecture and which is not already known corresponds to the following question:

Question   Does every digraph D without 2-cycles and out-degree at least 6 admit four vertex disjoint cycles?

Bibliography

[Alo96] N. Alon: Disjoint directed cycles, J. Combin. Theory Ser. B, 68(2):167--178, 1996. PDF

[BBT] J. Bang-Jensen, S. Bessy and S. Thomassé, Disjoint 3-cycles in tournaments: a proof of the Bermond-Thomassen conjecture for tournaments, J. Graph Theory, to appear.

*[BeTh81] J.-C. Bermond and C.~Thomassen: Cycles in digraphs---a survey, J. Graph Theory, 5(1):1--43, 1981. MathSciNet

[BLS07] S.~Bessy, N.~Lichiardopol, and J.-S. Sereni: Two proofs of the {B}ermond-{T}homassen conjecture for tournaments with bounded minimum in-degree, Discrete Math., Special Issue dedicated to CS06, to appear.

[LPS07] N.~Lichiardopol, A.~ P\'or, and J.-S. Sereni: A step towards the Bermond-Thomassen conjecture about disjoint cycles in digraphs, Submitted, 2007.

[Tho83] C.~Thomassen, Disjoint cycles in digraphs, Combinatorica, 3(3-4):393--396, 1983. MathSciNet


* indicates original appearance(s) of problem.
add new comment