 login/create account
login/create account
Porton, Victor
Several ways to apply a (multivalued) multiargument function to a family of filters ★★★
Author(s): Porton
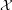 be an indexed family of filters on sets. Which of the below items are always pairwise equal?
be an indexed family of filters on sets. Which of the below items are always pairwise equal?
1. The funcoid corresponding to this function (considered as a single argument function on indexed families) applied to the reloidal product of filters 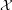 .
.
2. The funcoid corresponding to this function (considered as a single argument function on indexed families) applied to the starred reloidal product of filters 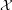 .
.
3. 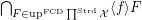 .
.
Keywords: funcoid; function; multifuncoid; staroid
Which outer reloids are equal to inner ones ★★
Author(s): Porton
Warning: This formulation is vague (not exact).
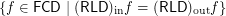 . In other words, simplify this formula.
. In other words, simplify this formula. The problem seems rather difficult.
Keywords:
A diagram about funcoids and reloids ★★
Author(s): Porton
Define for posets with order  :
:
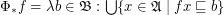 ;
;
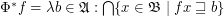 .
.
Note that the above is a generalization of monotone Galois connections (with 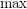 and
and  replaced with suprema and infima).
replaced with suprema and infima).
Then we have the following diagram:
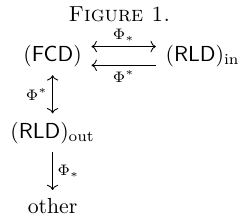
What is at the node "other" in the diagram is unknown.
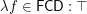 .
. 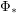 and
and 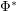 to "other" leads to? Particularly, does repeated applying
to "other" leads to? Particularly, does repeated applying 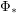 and/or
and/or 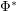 to the node "other" lead to finite or infinite sets?
to the node "other" lead to finite or infinite sets? Keywords: Galois connections
Outward reloid of composition vs composition of outward reloids ★★
Author(s): Porton
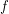 and
and 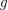
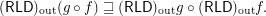
Keywords: outward reloid
A funcoid related to directed topological spaces ★★
Author(s): Porton
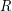 be the complete funcoid corresponding to the usual topology on extended real line
be the complete funcoid corresponding to the usual topology on extended real line ![$ [-\infty,+\infty] = \mathbb{R}\cup\{-\infty,+\infty\} $](/files/tex/3252019c60a83f00ff396d823dbff8040639f409.png) . Let
. Let 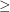 be the order on this set. Then
be the order on this set. Then 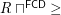 is a complete funcoid.
is a complete funcoid. 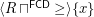 is the infinitely small right neighborhood filter of point
is the infinitely small right neighborhood filter of point ![$ x\in[-\infty,+\infty] $](/files/tex/4e57a21194d8d5a659e259a111ed13a9c23b52a1.png) .
. If proved true, the conjecture then can be generalized to a wider class of posets.
Keywords:
Infinite distributivity of meet over join for a principal funcoid ★★
Author(s): Porton
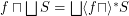 for principal funcoid
for principal funcoid 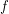 and a set
and a set  of funcoids of appropriate sources and destinations.
of funcoids of appropriate sources and destinations. Keywords: distributivity; principal funcoid
Entourages of a composition of funcoids ★★
Author(s): Porton
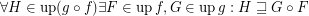 for every composable funcoids
for every composable funcoids 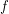 and
and 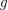 .
. Keywords: composition of funcoids; funcoids
What are hyperfuncoids isomorphic to? ★★
Author(s): Porton
Let  be an indexed family of sets.
be an indexed family of sets.
Products are 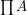 for
for 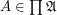 .
.
Hyperfuncoids are filters 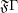 on the lattice
on the lattice 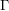 of all finite unions of products.
of all finite unions of products.
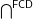 a bijection from hyperfuncoids
a bijection from hyperfuncoids 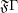 to:
to:- \item prestaroids on
 ; \item staroids on
; \item staroids on  ; \item completary staroids on
; \item completary staroids on  ?
? If yes, is 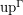 defining the inverse bijection? If not, characterize the image of the function
defining the inverse bijection? If not, characterize the image of the function 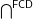 defined on
defined on 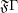 .
.
Consider also the variant of this problem with the set 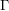 replaced with the set
replaced with the set 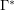 of complements of elements of the set
of complements of elements of the set 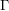 .
.
Keywords: hyperfuncoids; multidimensional
Another conjecture about reloids and funcoids ★★
Author(s): Porton
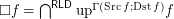 for reloid
for reloid 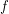 .
. 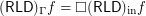 for every funcoid
for every funcoid 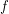 .
. Note: it is known that 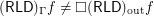 (see below mentioned online article).
(see below mentioned online article).
Keywords:

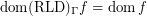 and
and 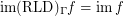 for every funcoid
for every funcoid  Drupal
Drupal CSI of Charles University
CSI of Charles University