 login/create account
login/create account
Porton, Victor
Funcoid corresponding to reloid through lattice Gamma ★★
Author(s): Porton
 and
and 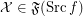 ,
, 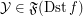 :
:- \item
![$ \mathcal{X} \mathrel{[(\mathsf{FCD}) f]} \mathcal{Y} \Leftrightarrow \forall F \in \operatorname{up}^{\Gamma (\operatorname{Src} f ; \operatorname{Dst} f)} f : \mathcal{X} \mathrel{[F]} \mathcal{Y} $](/files/tex/2f0c7dbaa1a5747d9bca753501374e8cd2500318.png) ; \item
; \item  .
. It's proved by me in this online article.
Keywords: funcoid corresponding to reloid
Restricting a reloid to lattice Gamma before converting it into a funcoid ★★
Author(s): Porton
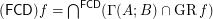 for every reloid
for every reloid 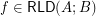 .
. Keywords: funcoid corresponding to reloid; funcoids; reloids
Inner reloid through the lattice Gamma ★★
Author(s): Porton
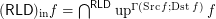 for every funcoid
for every funcoid  .
. Counter-example: 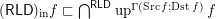 for the funcoid
for the funcoid 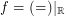 is proved in this online article.
is proved in this online article.
Keywords: filters; funcoids; inner reloid; reloids
Coatoms of the lattice of funcoids ★
Author(s): Porton
 and
and  be infinite sets. Characterize the set of all coatoms of the lattice
be infinite sets. Characterize the set of all coatoms of the lattice 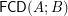 of funcoids from
of funcoids from  to
to  . Particularly, is this set empty? Is
. Particularly, is this set empty? Is 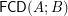 a coatomic lattice? coatomistic lattice?
a coatomic lattice? coatomistic lattice? Direct proof of a theorem about compact funcoids ★★
Author(s): Porton
 is a
is a  -separable (the same as
-separable (the same as 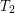 for symmetric transitive) compact funcoid and
for symmetric transitive) compact funcoid and  is a uniform space (reflexive, symmetric, and transitive endoreloid) such that
is a uniform space (reflexive, symmetric, and transitive endoreloid) such that  . Then
. Then 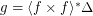 .
. The main purpose here is to find a direct proof of this conjecture. It seems that this conjecture can be derived from the well known theorem about existence of exactly one uniformity on a compact set. But that would be what I call an indirect proof, we need a direct proof instead.
The direct proof may be constructed by correcting all errors an omissions in this draft article.
Direct proof could be better because with it we would get a little more general statement like this:
 be a
be a  -separable compact reflexive symmetric funcoid and
-separable compact reflexive symmetric funcoid and  be a reloid such that
be a reloid such that- \item
 ; \item
; \item 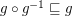 .
. Then 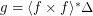 .
.
Keywords: compact space; compact topology; funcoid; reloid; uniform space; uniformity
Generalized path-connectedness in proximity spaces ★★
Author(s): Porton
Let  be a proximity.
be a proximity.
A set  is connected regarding
is connected regarding  iff
iff 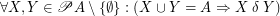 .
.
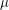 and a set
and a set 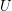 :
:- \item
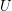 is connected regarding
is connected regarding 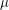 . \item For every
. \item For every  there exists a totally ordered set
there exists a totally ordered set 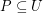 such that
such that 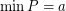 ,
, 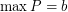 , and for every partion
, and for every partion 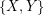 of
of  into two sets
into two sets 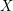 ,
, 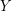 such that
such that 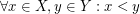 , we have
, we have ![$ X \mathrel{[ \mu]^{\ast}} Y $](/files/tex/0ef560be389646efd1fdde5ebc9afc9ac98ee64e.png) .
. Keywords: connected; connectedness; proximity space
Every monovalued reloid is metamonovalued ★★
Author(s): Porton
Keywords: monovalued
Every metamonovalued reloid is monovalued ★★
Author(s): Porton
Keywords:
Every metamonovalued funcoid is monovalued ★★
Author(s): Porton
The reverse is almost trivial: Every monovalued funcoid is metamonovalued.
Keywords: monovalued
Decomposition of completions of reloids ★★
Author(s): Porton
 and
and  it holds
it holds- \item
 if
if  is a co-complete reloid; \item
is a co-complete reloid; \item 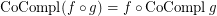 if
if  is a complete reloid; \item
is a complete reloid; \item 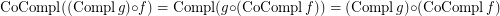 ; \item
; \item 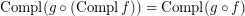 ; \item
; \item 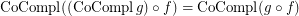 .
. Keywords: co-completion; completion; reloid

 Drupal
Drupal CSI of Charles University
CSI of Charles University