 login/create account
login/create account
connectivity
Forcing a $K_6$-minor ★★
Author(s): Barát ; Joret; Wood
Conjecture Every graph with minimum degree at least 7 contains a 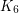 -minor.
-minor.
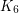 -minor.
-minor. Conjecture Every 7-connected graph contains a 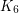 -minor.
-minor.
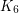 -minor.
-minor. Keywords: connectivity; graph minors
Chords of longest cycles ★★★
Author(s): Thomassen
Conjecture If  is a 3-connected graph, every longest cycle in
is a 3-connected graph, every longest cycle in  has a chord.
has a chord.
 is a 3-connected graph, every longest cycle in
is a 3-connected graph, every longest cycle in  has a chord.
has a chord. Keywords: chord; connectivity; cycle
Highly connected graphs with no K_n minor ★★★
Author(s): Thomas
Problem Is it true for all 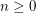 , that every sufficiently large
, that every sufficiently large  -connected graph without a
-connected graph without a 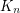 minor has a set of
minor has a set of 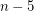 vertices whose deletion results in a planar graph?
vertices whose deletion results in a planar graph?
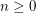 , that every sufficiently large
, that every sufficiently large  -connected graph without a
-connected graph without a 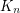 minor has a set of
minor has a set of 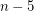 vertices whose deletion results in a planar graph?
vertices whose deletion results in a planar graph? Keywords: connectivity; minor

 Drupal
Drupal CSI of Charles University
CSI of Charles University