 login/create account
login/create account
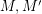 be abelian groups and let
be abelian groups and let 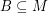 and
and 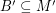 satisfy
satisfy 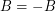 and
and  . If there is a homomorphism from
. If there is a homomorphism from 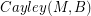 to
to 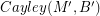 , then every graph with a B-flow has a B'-flow.
, then every graph with a B-flow has a B'-flow. Definition:Let  be a directed graph, Let
be a directed graph, Let  be an abelian group, and let
be an abelian group, and let  be a subset of
be a subset of  such that
such that 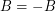 . We say that a flow or a tension
. We say that a flow or a tension 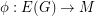 is a
is a  -flow or a
-flow or a  -tension if the range is a subset of
-tension if the range is a subset of  . If
. If 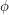 is a
is a  -flow (
-flow ( -tension) of
-tension) of  and we reverse the direction of the edge
and we reverse the direction of the edge  , then we may obtain a new
, then we may obtain a new  -flow (
-flow ( -tension) by changing
-tension) by changing 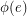 to
to 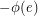 . Thus, the existence of a
. Thus, the existence of a  -flow or
-flow or  -tension does not depend on the orientation, and we say that an undirected graph has a
-tension does not depend on the orientation, and we say that an undirected graph has a  -flow or a
-flow or a  -tension if some (and thus every) orientation of it admits such a map. We define the Cayley graph
-tension if some (and thus every) orientation of it admits such a map. We define the Cayley graph 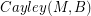 to be the simple graph with vertex set
to be the simple graph with vertex set  in which two vertices
in which two vertices 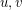 are joined by an edge if and only if
are joined by an edge if and only if 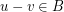 .
.
It is well known that a graph has a  -tension if and only if it has a homomorphism to
-tension if and only if it has a homomorphism to 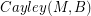 . So, if
. So, if 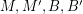 are as in the conjecture and there is a homomorphism from
are as in the conjecture and there is a homomorphism from 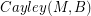 to
to 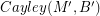 , then every graph G with a
, then every graph G with a  -tension has a
-tension has a 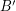 -tension. This follows from the previous sentence and the fact that the composition of two homomorphisms is another homomorphism. In essence, the above conjecture states that the same equivalence should hold true for flows.
-tension. This follows from the previous sentence and the fact that the composition of two homomorphisms is another homomorphism. In essence, the above conjecture states that the same equivalence should hold true for flows.
If  and
and 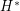 are directed planar dual graphs (each edge of
are directed planar dual graphs (each edge of 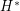 crosses left to right over the corresponding edge of
crosses left to right over the corresponding edge of  ), then a map
), then a map  is a tension if and only if the dual map
is a tension if and only if the dual map 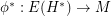 (
( is given by the rule
is given by the rule 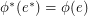 ) is a flow of
) is a flow of 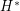 . Thus, planar duality exchanges flows and tensions. For two undirected planar dual graphs,
. Thus, planar duality exchanges flows and tensions. For two undirected planar dual graphs,  and
and 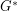 we have that G has a
we have that G has a  -flow if and only if
-flow if and only if 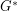 has a
has a  -tension. It follows from this duality and the observation from the previous paragraph, that the above conjecture is true for planar graphs.
-tension. It follows from this duality and the observation from the previous paragraph, that the above conjecture is true for planar graphs.
This conjecture is also known in the special case when 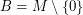 and
and  . In this case,
. In this case, 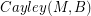 and
and 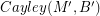 are the complete graphs on
are the complete graphs on 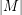 and
and 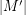 vertices respectively, so there is a homomorphism from
vertices respectively, so there is a homomorphism from 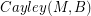 to
to 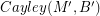 if and only if
if and only if 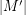 is greater than or equal to
is greater than or equal to 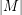 . Thus, in this case the conjecture is equivalent to the assertion that every graph with a nowhere-zero
. Thus, in this case the conjecture is equivalent to the assertion that every graph with a nowhere-zero  -flow also has a nowhere-zero
-flow also has a nowhere-zero 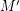 -flow if
-flow if 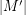 is at least
is at least 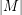 . This statement is true by a result of Tutte.
. This statement is true by a result of Tutte.

 Drupal
Drupal CSI of Charles University
CSI of Charles University